Question

【题目】已知函数f（x）=|x2﹣1|+x2﹣kx．
（1）若k=2时，求出函数f（x）的单调区间及最小值；
（2）若f（x）≥0恒成立，求实数k的取值范围．

Answer 1

【答案】
（1）解：k=2时，f（x）= ，

当x＜﹣1或x＞1时，y=2x2﹣2x﹣1=2（x﹣ ）2﹣ ，f（x）在（﹣∞，﹣1）单调递减，在（1，+∞）单调递增；

当﹣1≤x≤1时，f（x）=1﹣2x单调递减；

综上，f（x）在（﹣∞，1）单调递减，在（1，+∞）单调递增；

所以f（x）min=f（1）=﹣1

（2）解：f（x）= ，

当﹣1≤x≤1时，1﹣kx≥0恒成立，令g（x）=1﹣kx，则 ，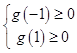

解得：﹣1≤k≤1；

当x＞1时，k≤2x﹣ 恒成立，y=2x﹣ 在（1，+∞）单调递增，解得k≤1；

当x＜1时，k≥2x﹣ 恒成立，同理解得k≥﹣1．

综上，﹣1≤k≤1．

【解析】（1）若k=2时，f（x）= ，利用二次函数的性质可求出函数f（x）的单调区间及最小值；（2）若f（x）≥0恒成立，分﹣1≤x≤1、x＞1与x＜1三类讨论，分别构造函数，利用函数的单调性求得k的取值范围，最后取交集即可求得实数k的取值范围．