练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在△ABC中，射影定理可表示为a＝b·cosC＋c·cosB．其中a，b，c分别为角A，B，C的对边，类比上述定理．写出对空间四面体性质的猜想．

    【答案】见解析

    【解析】试题分析：这是一个升维类比，边长类比面积，线线角类比为面面角，将平面中的三角形类比成空间中的三棱锥。

    试题解析：在四面体P－ABC中，S1，S2，S3、S分别表示△PAB，△PBC，△PCA，△ABC的面积，α，β，γ依次表示面PAB，面PBC，面PCA与底面ABC所成角的大小，我们猜想将射影定理类比推理到三维空间，其表现形式应为S＝S1cosα＋S2cosβ＋S3cosγ.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

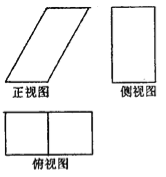
    【题目】一个几何体的三视图如图所示，已知正（主）视图是底边长为1的平行四边形，侧（左）视图是一个长为，宽为1的矩形，俯视图为两个边长为1的正方形拼成的矩形．

    （1）求该几何体的体积；

    （2）求该几何体的表面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列说法错误的是（ ）

    A. 平行于同一个平面的两个平面平行

    B. 平行于同一直线的两个平面平行

    C. 垂直于同一个平面的两条直线平行

    D. 垂直于同一条直线的两个平面平行

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某公司生产一种产品，每年需投入固定成本25万元，此外每生产1件这样的产品，还需增加投入0.5万元，经市场调查知这种产品年需求量为500件，产品销售数量为t件时，销售所得的收入为万元.

    （1）该公司这种产品的年生产量为x件，生产并销售这种产品所得到的利润关于当年产量x的函数为f（x），求f（x）；

    （2）当该公司的年产量为多少件时，当年所获得的利润最大

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设定义在上的函数对于任意实数，都有成立，且，当时，．

    （1）判断的单调性，并加以证明；

    （2）试问：当时，是否有最值?如果有，求出最值；如果没有，说明理由；

    （3）解关于的不等式，其中．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（1）已知函数在上具有单调性，求实数的取值范围.

    （2）关于x的方程mx2+2（m+3）x+2m+14=0有两个不同的实根,且一个大于4,另一个小于4,求m的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】由两点确定的直线中,斜率不存在的是

    A．(4,2)与(-4,1) B．(0,3)与(3,0)

    C．(3,-1)与(2, -1) D．(-2,2)与(-2,5)

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）求函数的单调区间和极值；

    （2）证明：当时，函数没有零点（提示：）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列结论正确的是（ ）

    ①函数关系是一种确定性关系；

    ②相关关系是一种非确定性关系；

    ③回归分析是对具有函数关系的两个变量进行统计分析的一种方法；

    ④回归分析是对具有相关关系的两个变量进行统计分析的一种常用方法．

    A. ①② B. ①②③ C. ①②④ D. ①②③④

    查看答案和解析>>

    同步练习册答案