
分析 对于命题P:对任意实数x都有ax2+ax+1>0恒成立?a=0或$\left\{\begin{array}{l}{a>0}\\{△<0}\end{array}\right.$,解得a即可;对于命题Q:关于x的方程x2-x+a=0有实数根?△=1-4a≥0,解得a即可.由于¬p∨Q为假命题,可得P为真命题,Q为假命题,求其交集即可.
解答 解:对于命题P:对任意实数x都有ax2+ax+1>0恒成立?a=0或$\left\{\begin{array}{l}{a>0}\\{△<0}\end{array}\right.$,解得0≤a<4;
对于命题Q:关于x的方程x2-x+a=0有实数根,?△=1-4a≥0,解得a≤$\frac{1}{4}$.
∵¬p∨Q为假命题,
∴P为真命题,Q为假命题,
∴0≤a<4且a$>\frac{1}{4}$;
解得$\frac{1}{4}<a<4$.
所以实数a的取值范围为$(\frac{1}{4},4)$.
点评 本题考查了复合命题真假的判定方法、二次函数的性质、一元二次方程有实数根的充要条件,考查了推理能力与计算能力,属于中档题.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
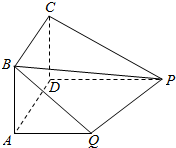 如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB=$\frac{1}{2}$PD=1.
如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB=$\frac{1}{2}$PD=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4$\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 等腰三角形 | B. | 直角三角形 | ||
| C. | 等边三角形 | D. | 等腰或直角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| P(X2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com