
【题目】已知定义域为![]() 的函数
的函数![]() 是奇函数.
是奇函数.
(1)求![]() 的值;
的值;
(2)判断函数![]() 的单调性并证明;
的单调性并证明;
(2)若关于![]() 的不等式
的不等式![]() 在
在![]() 有解,求实数
有解,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)见解析(3)
(2)见解析(3)![]()
【解析】试题分析:(1)由![]() 为奇函数可知,
为奇函数可知, ![]() ,即可得解;
,即可得解;
(2)由![]() 递增可知
递增可知![]() 在
在![]() 上为减函数,对于任意实数
上为减函数,对于任意实数![]() ,不妨设
,不妨设![]() ,化简
,化简![]() 判断正负即可证得;
判断正负即可证得;
(3)不等式![]() ,等价于
,等价于![]() ,即
,即![]() ,原问题转化为
,原问题转化为![]() 在
在![]() 上有解,求解
上有解,求解![]() 的最大值即可.
的最大值即可.
试题解析
解:(1)由![]() 为奇函数可知,
为奇函数可知, ![]() ,解得
,解得![]() .
.
(2)由![]() 递增可知
递增可知![]() 在
在![]() 上为减函数,
上为减函数,
证明:对于任意实数![]() ,不妨设
,不妨设![]() ,
,
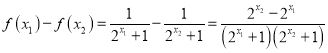
∵![]() 递增,且
递增,且![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() ,故
,故![]() 在
在![]() 上为减函数.
上为减函数.
(3)关于![]() 的不等式
的不等式![]() ,
,
等价于![]() ,即
,即![]() ,
,
因为![]() ,所以
,所以![]() ,
,
原问题转化为![]() 在
在![]() 上有解,
上有解,
∵![]() 在区间
在区间![]() 上为减函数,
上为减函数,
∴![]() ,
, ![]() 的值域为
的值域为![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴![]() 的取值范围是
的取值范围是![]() .
.
点晴:本题属于对函数单调性应用的考察,若函数![]() 在区间上单调递增,则
在区间上单调递增,则![]() 时,有
时,有![]() ,事实上,若
,事实上,若![]() ,则
,则![]() ,这与
,这与![]() 矛盾,类似地,若
矛盾,类似地,若![]() 在区间上单调递减,则当
在区间上单调递减,则当![]() 时有
时有![]() ;据此可以解不等式,由函数值的大小,根据单调性就可以得自变量的大小关系.本题中可以利用对称性数形结合即可.
;据此可以解不等式,由函数值的大小,根据单调性就可以得自变量的大小关系.本题中可以利用对称性数形结合即可.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
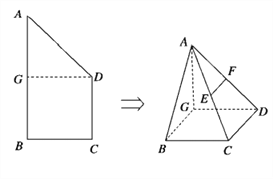
【题目】如图,在直角梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为线段
为线段![]() 的中点,将
的中点,将![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() ,得到几何体
,得到几何体![]() .
.
(1)若![]() 分别为线段
分别为线段![]() 的中点,求证:
的中点,求证: ![]() 平面
平面![]() ;
;
(2)求证: ![]() 平面
平面![]() ;
;
(3)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加高二年级期末考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后得到如下频率分布表.根据相关信息回答下列问题: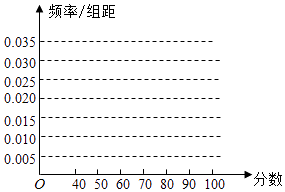
(1)求a,b的值,并画出频率分布直方图;
(2)统计方法中,同一组数据常用该组区间的中点值作为代表,据此估计本次考试的平均分;
(3)用分层抽样的方法在分数在[60,80)内学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2人,求至多有1人的分数在[70,80)内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了普及环保知识,增强环保意识,某校从理科甲班抽取60人,从文科乙班抽取50人参加环保知识测试.
(Ⅰ)根据题目条件完成下面2×2列联表,并据此判断是否有99%的把握认为环保知识成绩优秀与学生的文理分类有关.
优秀人数 | 非优秀人数 | 总计 | |
甲班 | |||
乙班 | 30 | ||
总计 | 60 |
(Ⅱ)现已知A,B,C三人获得优秀的概率分别为 ![]() ,设随机变量X表示A,B,C三人中获得优秀的人数,求X的分布列及期望E(X).
,设随机变量X表示A,B,C三人中获得优秀的人数,求X的分布列及期望E(X).
附: ![]() ,n=a+b+c+d
,n=a+b+c+d
P(K2>k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种商品的市场需求量![]() (万件)、市场供应量
(万件)、市场供应量![]() (万件)与市场价格
(万件)与市场价格![]() (元/件)分别近似地满足下列关系:
(元/件)分别近似地满足下列关系: ![]() ,
, ![]() .当
.当![]() 时的市场价格称为市场平衡价格,此时的需求量称为平衡需求量.
时的市场价格称为市场平衡价格,此时的需求量称为平衡需求量.
(1)求平衡价格和平衡需求量;
(2)若该商品的市场销售量![]() (万件)是市场需求量
(万件)是市场需求量![]() 和市场供应量
和市场供应量![]() 两者中的较小者,该商品的市场销售额
两者中的较小者,该商品的市场销售额![]() (万元)等于市场销售量
(万元)等于市场销售量![]() 与市场价格
与市场价格![]() 的乘积.
的乘积.
①当市场价格![]() 取何值时,市场销售额
取何值时,市场销售额![]() 取得最大值;
取得最大值;
②当市场销售额![]() 取得最大值时,为了使得此时的市场价格恰好是新的市场平衡价格,则政府应该对每件商品征税多少元?
取得最大值时,为了使得此时的市场价格恰好是新的市场平衡价格,则政府应该对每件商品征税多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求函数![]() 的定义域;
的定义域;
(2)判断![]() 的奇偶性;
的奇偶性;
(3)方程![]() 是否有实根?如果有实根
是否有实根?如果有实根![]() ,请求出一个长度为
,请求出一个长度为![]() 的区间
的区间![]() ,使
,使![]() ;如果没有,请说明理由(注:区间
;如果没有,请说明理由(注:区间![]() 的长度
的长度![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为![]() 的函数
的函数![]() 是奇函数
是奇函数
(Ⅰ)求![]() 值;
值;
(Ⅱ)判断并证明该函数在定义域![]() 上的单调性;
上的单调性;
(Ⅲ)若对任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(Ⅳ)设关于![]() 的函数
的函数![]() 有零点,求实数
有零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知方程![]() .
.
(Ⅰ)若此方程表示圆,求![]() 的取值范围;
的取值范围;
(Ⅱ)若(Ⅰ)中的圆与直线![]() 相交于
相交于![]() ,
, ![]() 两点,且
两点,且![]() (
(![]() 为坐标原点),求
为坐标原点),求![]() ;
;
(Ⅲ)在(Ⅱ)的条件下,求以![]() 为直径的圆的方程.
为直径的圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
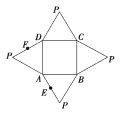
【题目】下图是一几何体的平面展开图,其中四边形![]() 为正方形,
为正方形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为全等的等边三角形,
为全等的等边三角形, ![]() 分别为
分别为![]() 的中点.在此几何体中,下列结论中错误的为( )
的中点.在此几何体中,下列结论中错误的为( )
A. 直线![]() 与直线
与直线![]() 共面 B. 直线
共面 B. 直线![]() 与直线
与直线![]() 是异面直线
是异面直线
C. 平面![]() 平面
平面![]() D. 面
D. 面![]() 与面
与面![]() 的交线与
的交线与![]() 平行
平行
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com