
分析 (I)设出等差数列的公差,利用已知条件,列出方程,即可求解数列{an}的通项公式;
(II)数列$\{{a_n}•{2^{a_n}}\}$的表达式,利用错位相减法求解数列的前n项.
解答 解:( I)设公差为d,由已知得$\left\{\begin{array}{l}2{a_2}+{a_3}+{a_5}{=4}{a_1}{+8}d{=20}\\ 10{a_1}{+}\frac{{{10}×{9}}}{2}d{=10}{a_1}{+45}d{=100}\end{array}\right.$,(2分)
解得$\left\{\begin{array}{l}{a_1}=1\\ d=2\end{array}\right.$,(4分)
所以{an}的通项公式为an=5+2(n-3)=2n-1,(5分)
( II)由( I)可知${a_n}•{b_n}=(2n-1)×{2^{2n-1}}$,
所以${S_n}=1×{2^1}+3×{2^3}+5×{2^5}+…+(2n-3)×{2^{2n-3}}+(2n-1)×{2^{2n-1}}$,①$4{S_n}=1×{2^3}+3×{2^5}+5×{2^7}+…+(2n-3)×{2^{2n-1}}+(2n-1)×{2^{2n+1}}$,②(7分)
①-②得:$-3{S_n}=2+2×({2^3}+{2^5}+…+{2^{2n-1}})-(2n-1)×{2^{2n+1}}$,
∴${S_n}=\frac{{2+2×({2^3}+{2^5}+…+{2^{2n-1}})-(2n-1)×{2^{2n+1}}}}{-3}$(9分)
=$\frac{{2+2×(\frac{{8(1-{4^{n-1}})}}{1-4})-(2n-1)×{2^{2n+1}}}}{-3}$
=$\frac{{-6+2×8(1-{4^{n-1}})+(6n-3)×{2^{2n+1}}}}{9}$(11分)
=$\frac{{10+(6n-5)×{2^{2n+1}}}}{9}$(12分)
点评 本题考查等差数列的性质,错位相减法求解数列的和的方法,考查计算能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
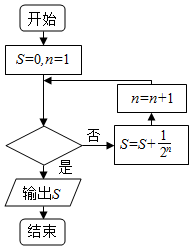
| A. | n≥12? | B. | n≥11? | C. | n≥10? | D. | n≥9? |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com