
已知函数 .
.
(Ⅰ)若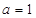 ,求函数
,求函数 的单调区间和极值;
的单调区间和极值;
(Ⅱ)设函数 图象上任意一点的切线
图象上任意一点的切线 的斜率为
的斜率为 ,当
,当 的最小值为1时,求此时切线
的最小值为1时,求此时切线 的方程.
的方程.
(Ⅰ) 的单调递增区间为
的单调递增区间为 ,
, ;单调递减区间为
;单调递减区间为 ;
; 极大值为
极大值为 ;极小值为
;极小值为 ; (Ⅱ)切线
; (Ⅱ)切线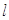 的方程为:
的方程为: .
.
解析试题分析:(Ⅰ)注意, 的定义域为(
的定义域为( ).将
).将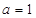 代入
代入 ,求导得:
,求导得: .由
.由 得
得 ,或
,或 ,由
,由 得
得 ,由此得
,由此得 的单调递增区间为
的单调递增区间为 ,
, ;单调递减区间为
;单调递减区间为 ,进而可得
,进而可得 极大值为
极大值为 ;极小值为
;极小值为 . (Ⅱ)求导,再用重要不等式可得导数的最小值,即切线斜率的最小值:
. (Ⅱ)求导,再用重要不等式可得导数的最小值,即切线斜率的最小值: ,由此得
,由此得 .由
.由 ,即
,即 得
得 ,所以切点为
,所以切点为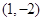 ,由此可得切线的方程.
,由此可得切线的方程.
试题解析:(Ⅰ) 的定义域为(
的定义域为( )时, 1分
)时, 1分
当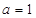 时,
时, 2分
2分
由 得
得 ,
,
由 得
得 ,或
,或 ,由
,由 得
得 , 3分
, 3分
∴ 的单调递增区间为
的单调递增区间为 ,
, ;单调递减区间为
;单调递减区间为 5分
5分
∴ 极大值为
极大值为 ;极小值为
;极小值为 7分
7分
(Ⅱ)由题意知 ∴
∴ 9分
9分
此时 ,即
,即 ,∴
,∴ ,切点为
,切点为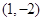 , 11分
, 11分
∴此时的切线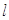 方程为:
方程为: . 13分
. 13分
考点:导数的应用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
已知函数f(x)=- x3+
x3+ x2-2x(a∈R).
x2-2x(a∈R).
(1)当a=3时,求函数f(x)的单调区间;
(2)若对于任意x∈[1,+∞)都有f′(x)<2(a-1)成立,求实数a的取值范围;
(3)若过点 可作函数y=f(x)图象的三条不同切线,求实数a的取值范围.
可作函数y=f(x)图象的三条不同切线,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=ax+ln x,g(x)=ex.
(1)当a≤0时,求f(x)的单调区间;
(2)若不等式g(x)<  有解,求实数m的取值范围.
有解,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲方是一农场,乙方是一工厂.由于乙方生产需占用甲方的资源,因此甲方有权向乙方索赔以弥补经济损失并获得一定净收入,在乙方不赔付甲方的情况下,乙方的年利润x(元)与年产量t(吨)满足函数关系x=2 000 .若乙方每生产一吨产品必须赔付甲方S元(以下称S为赔付价格).
.若乙方每生产一吨产品必须赔付甲方S元(以下称S为赔付价格).
(1)将乙方的年利润w(元)表示为年产量t(吨)的函数,并求出乙方获得最大利润的年产量;
(2)甲方每年受乙方生产影响的经济损失金额y=0.002t2(元),在乙方按照获得最大利润的产量进行生产的前提下,甲方要在索赔中获得最大净收入,应向乙方要求的赔付价格S是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com