
如图,在底面边长为1,侧棱长为2的正四棱柱 中,P是侧棱
中,P是侧棱 上的一点,
上的一点, .
.
(1)试确定m,使直线AP与平面BDD1B1所成角为60º;
(2)在线段 上是否存在一个定点
上是否存在一个定点 ,使得对任意的m,
,使得对任意的m,
 ⊥AP,并证明你的结论.
⊥AP,并证明你的结论.

(1)60º. (2)Q为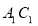 的中点
的中点
【解析】
试题分析:(1)利用空间向量研究线面角,关键在于正确表示各点坐标,正确求出平面一个法向量,正确理解线面角与向量夹角之间互余的关系. 建立空间直角坐标系,则A(1,0,0), B(1,1,0), P(0,1,m),C(0,1,0), D(0,0,0), B1(1,1,1), D1(0,0,2). 所以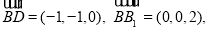
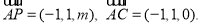 又由
又由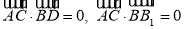 知
知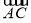 为平面
为平面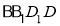 的一个法向量.
的一个法向量. 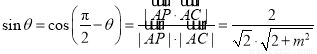 =
=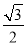 ,解得
,解得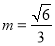 (2)同(1)若在
(2)同(1)若在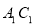 上存在这样的点Q,设此点的横坐标为x,则
上存在这样的点Q,设此点的横坐标为x,则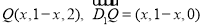 .
.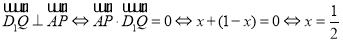 ,即Q为
,即Q为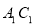 的中点.
的中点.
(1)建立空间直角坐标系,则
A(1,0,0), B(1,1,0), P(0,1,m),C(0,1,0), D(0,0,0),
B1(1,1,1), D1(0,0,2).所以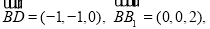
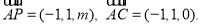 又由
又由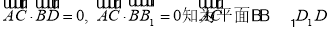 的一个法向量.设
的一个法向量.设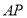 与
与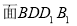 所成的角为
所成的角为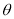 ,
,
则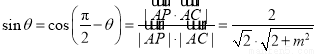 =
=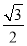 , 5分
, 5分
解得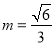 .故当
.故当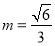 时,直线AP与平面
时,直线AP与平面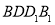 所成角为60º. 7分
所成角为60º. 7分
(2)若在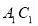 上存在这样的点Q,设此点的横坐标为x,
上存在这样的点Q,设此点的横坐标为x,
则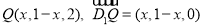 .
.
依题意,对任意的m要使D1Q在平面APD1上的射影垂直于AP. 等价于
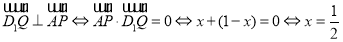
即Q为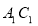 的中点时,满足题设的要求. 14分
的中点时,满足题设的要求. 14分
考点:利用空间向量研究线面关系


科目:高中数学 来源:2015届江苏省南京市高二下4月月考数学试卷(解析版) 题型:填空题
为了分析某篮球运动员在比赛中发挥的稳定程度,统计了该运动员在6场比赛中的得分,用茎叶图表示如右图,则该组数据的方差为___________.

查看答案和解析>>
科目:高中数学 来源:2015届江苏省南京外国语学校高二上学期期中测试数学试卷(解析版) 题型:解答题
已知函数 .
.
(1)若曲线 的一条切线的斜率是2,求切点坐标;
的一条切线的斜率是2,求切点坐标;
(2)求 在点
在点 处的切线方程.
处的切线方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com