
| A. | α=$\frac{π}{3}$,β=-$\frac{π}{3}$ | B. | α=$\frac{π}{3}$,β=$\frac{2π}{3}$ | C. | α=$\frac{π}{5}$,β=-$\frac{7π}{10}$ | D. | α=$\frac{π}{3}$,β=-$\frac{π}{6}$ |
分析 根据向量的平行的条件以及两角和的余弦公式即可判断.
解答 解:向量$\overrightarrow{a}$=(cosα,sinβ),$\overrightarrow{b}$=(sinα,cosβ),若$\overrightarrow{a}$∥$\overrightarrow{b}$,
∴cosαcosβ-sinαsinβ=0,
即cos(α+β)=0,
∴α+β=kπ+$\frac{π}{2}$,k∈Z,
对于A:α+β=0,不符合,
对于B,α+β=π,不符合,
对于C:α+β=-$\frac{π}{2}$,符合,
对于D,α+β=$\frac{π}{6}$,不符合,
故选:C.
点评 本题考查了向量的平行的条件以及两角和的余弦公式,属于基础题.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | -4 | C. | -3 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{18}$ | B. | $\frac{9}{32}$ | C. | $\frac{23}{32}$ | D. | $\frac{17}{18}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
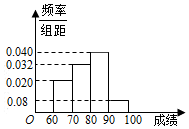 某学校为了宣传环保知识,举办了“环保知识竞赛”活动
某学校为了宣传环保知识,举办了“环保知识竞赛”活动| 年级 | 抽取份数 | 优秀人数 | 优秀率 |
| 高一 | 40 | a | 0.5 |
| 高二 | n | 18 | 0.6 |
| 高三 | 30 | 21 | b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
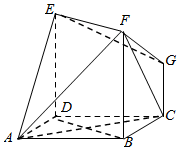 如图,矩形BDEF垂直于正方形ABCD,GC垂直于平面ABCD,且AB=DE=2CG=2.
如图,矩形BDEF垂直于正方形ABCD,GC垂直于平面ABCD,且AB=DE=2CG=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com