练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
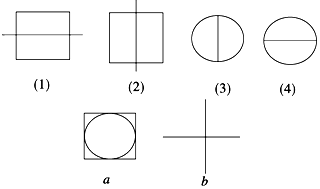
    2．定义A*B，B*C，C*D，D*A的运算分别对应下面图中的（1），（2），（3），（4），则图中，a，b对应的运算是（　　）
    A．B*D，A*DB．B*D，A*CC．B*C，A*DD．C*D，A*D

    分析 根据已知图象与运算的关系，进行必要的分析归纳，找出规律，猜想未知的图象与运算的关系

    解答 解：根据题意可知A对应横线，B对应矩形，C对应竖线，D对应圆．故选B．

    点评 本题考查了归纳推理，归纳推理的一般步骤是：（1）通过观察个别情况发现某些相同性质；（2）从已知的相同性质中推出一个明确表达的一般性命题（猜想），属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    12．已知$α∈（{\frac{π}{4}\;，\;\;\frac{π}{2}}）$，化简$\sqrt{1+sinα}+\sqrt{1-sinα}-\sqrt{2+2cosα}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

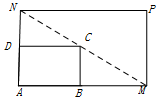    13．如图所示，将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN，要求M在AB的延长线上，N在AD的延长线上，且对角线MN过C点．已知AB=2米，AD=1米．
    （1）设BM=x（单位：米）．写出花坛AMPN的面积为S关于x的函数关系式S=f（x）；
    （2）判断S=f（x）的单调性，并用单调性定义证明，求当AM，AN的长度分别是多少时，花坛AMPN的面积最小？

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．下面有段演绎推理：
    “直线平行于平面，则该直线平行于平面内所有直线；
    已知直线b?平面α，直线a?平面α，直线b∥平面α，
    则直线b∥直线a”，则该推理中（　　）
    A．大前提错误B．小前提错误C．推理形式错误D．该推理是正确的

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．将边长为$\sqrt{2}$的正方形ABCD沿对角线AC折成一个直二面角B-AC-D．则四面体ABCD的内切球的半径为（　　）
    A．1B．$2\sqrt{2}-\sqrt{3}$C．$\sqrt{2}-1$D．$2-\sqrt{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．曲线C的极坐标方程为：ρ=2cosθ，曲线T的参数 方程为$\left\{\begin{array}{l}x=-t+1\\ y=2t+1\end{array}\right.$（t为参数），则曲线C与T的公共点有2个．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

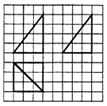    14．如图，网格纸上小正方形的边长为1，粗实线画出的是某四棱锥的三视图，则该四棱锥的外接球的表面积为（　　）
    A．136πB．34πC．25πD．18π

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

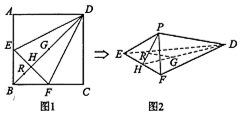    11．如图l，在正方形ABCD中，点E，F分别是AB，BC的中点，BD与EF交于点H，点G，R分别在线段DH，HB上，且$\frac{DG}{GH}$=$\frac{BR}{RH}$．将△AED，△CFD，△BEF分别沿DE，DF，EF折起，使点A，B，C重合于点P，如图2所示，
    （I）求证：GR⊥平面PEF；
    （Ⅱ）若正方形ABCD的边长为4，求三棱锥P-DEF的内切球的半径．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

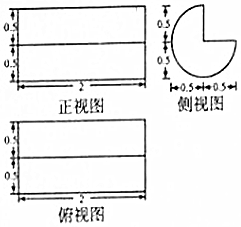    12．某同学在运动场所发现一实心椅子，其三视图如图所示（俯视图是圆的一部分及该圆的两条互相垂直的半径，有关尺寸如图，单位：m），经了解，建造该类椅子的平均成本为240元/m3，那么该椅子的建造成本约为（π≈3.14）（　　）
    A．94.20元B．240.00元C．282.60元D．376.80元

    查看答案和解析>>

    同步练习册答案