
科目:高中数学 来源:2014-2015学年辽宁省朝阳市三校协作体高三下学期开学联考理科数学试卷(解析版) 题型:解答题
如图,在三棱柱 中,已知
中,已知 ,
,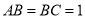 ,
,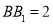 ,
,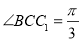 .
.

(1)求证: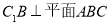 ;
;
(2)设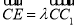 (
(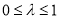 ),且平面
),且平面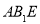 与
与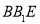 所成的锐二面角的大小为30°,试求的值.
所成的锐二面角的大小为30°,试求的值.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省苏锡常镇四市高三教学情况调研一理科数学试卷(解析版) 题型:解答题
在极坐标系中,曲线C的极坐标方程为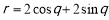 ,以极点为坐标原点,极轴为
,以极点为坐标原点,极轴为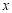 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线 的参数方程为
的参数方程为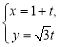 (
( 为参数),求直线
为参数),求直线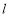 被曲线
被曲线 所截得的弦长.
所截得的弦长.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省苏锡常镇四市高三教学情况调研一理科数学试卷(解析版) 题型:填空题
如图,四棱锥P-ABCD中,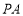 ⊥底面
⊥底面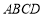 ,底面
,底面 是矩形,
是矩形,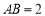 ,
,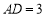 ,
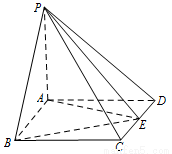
, ,
,
点E为棱CD上一点,则三棱锥E-PAB的体积为 .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖南省怀化市小学课改质量检测高三第一次模考理科数学试卷(解析版) 题型:解答题
(本题满分13分)
已知圆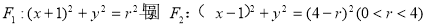 的公共点的轨迹为曲线
的公共点的轨迹为曲线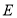 ,且曲线
,且曲线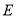 与
与 轴的正半轴相交于点
轴的正半轴相交于点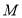 .若曲线
.若曲线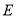 上相异两点
上相异两点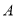 、
、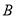 满足直线
满足直线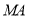 ,
,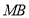 的斜率之积为
的斜率之积为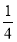 .
.
(Ⅰ)求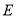 的方程;
的方程;
(Ⅱ)证明直线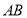 恒过定点,并求定点的坐标;
恒过定点,并求定点的坐标;
(Ⅲ)求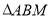 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖南省怀化市小学课改质量检测高三第一次模考理科数学试卷(解析版) 题型:选择题
设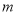 ,
,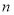 是两条不同的直线,
是两条不同的直线, ,
,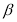 ,
,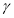 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题:
①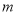 ⊥
⊥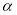 ,
,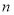 ∥
∥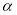 ,则
,则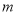 ⊥
⊥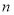 ;
;
②若 ⊥
⊥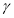 ,
,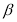 ⊥
⊥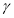 ,则
,则 ∥
∥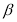 ;
;
③若 ∥
∥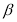 ,
,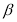 ∥
∥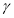 ,
, 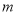 ⊥
⊥ ,则
,则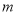 ⊥
⊥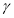 ;
;
④若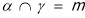 ,
,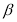

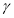 =
=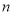 ,
,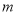 ∥
∥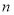 ,则
,则 ∥
∥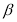 .
.
其中正确命题的序号是
A.①和③ B.②和③ C.③和④ D.①和④
查看答案和解析>>
科目:高中数学 来源:2014-2015学年福建省龙岩市高三教学质量检查文科数学试卷(解析版) 题型:选择题
已知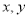 满足
满足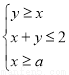 ,且目标函数
,且目标函数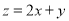 的最小值为
的最小值为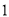 ,则实数
,则实数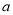 的值是( )
的值是( )
A.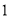 B.
B.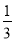 C.
C.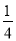 D.
D.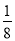
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com