
| A. | $cos(2x-\frac{π}{6})$ | B. | $sin(2x-\frac{π}{6})$ | C. | $cos(2x-\frac{π}{3})$ | D. | $sin(2x-\frac{π}{3})$ |
科目:高中数学 来源: 题型:解答题
 某特色餐馆开通了美团外卖服务,在一周内的某特色外卖份数x(份)与收入y(元)之间有如下的对应数据:
某特色餐馆开通了美团外卖服务,在一周内的某特色外卖份数x(份)与收入y(元)之间有如下的对应数据:| 外卖份数x(份) | 2 | 4 | 5 | 6 | 8 |
| 收入y(元) | 30 | 40 | 60 | 50 | 70 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
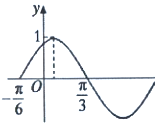 函数$f(x)=Asin({ωx+φ})({x∈R,A>0,ω>0,|φ|<\frac{π}{2}})$的部分图象如图所示,如果${x_1},{x_2}∈({-\frac{π}{6},\frac{π}{3}})$,且f(x1)=f(x2),则f(x1+x2)=( )
函数$f(x)=Asin({ωx+φ})({x∈R,A>0,ω>0,|φ|<\frac{π}{2}})$的部分图象如图所示,如果${x_1},{x_2}∈({-\frac{π}{6},\frac{π}{3}})$,且f(x1)=f(x2),则f(x1+x2)=( )| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-3,-2,4) | B. | (3,-2,-4) | C. | (-3,2,-4) | D. | (-3,2,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com