
分析 (1)把圆C的方程x2+y2-2x+4y-3=0化为标准方程为(x-1)2+(y+2)2=8,得到圆心为C(1,-2)和半径,由圆心C到直线l的距离等于圆的半径列出方程,求解即可得实数t的值;
(2)由(1)知,圆心到直线l的距离$d=\frac{|3+t|}{\sqrt{2}}$,且|MN|=4,r2=8,解得d,进一步求出实数t的值.
解答 解:圆C的方程x2+y2-2x+4y-3=0化为标准方程为(x-1)2+(y+2)2=8,
故圆心为C(1,-2),且半径$r=2\sqrt{2}$,
(1)∵直线l与圆C相切,∴圆心C到直线l的距离等于圆的半径,
即$\frac{|1-(-2)+t|}{\sqrt{1+(-1)^{2}}}=2\sqrt{2}$,整理得|3+t|=4,解得t=1或t=-7;
(2)由(1)知,圆心到直线l的距离$d=\frac{|3+t|}{\sqrt{2}}$,
又|MN|=$2\sqrt{{r}^{2}-{d}^{2}}=4$,r2=8,解得d=2,∴$\frac{|3+t|}{\sqrt{2}}=2$即$t=-3±2\sqrt{2}$.
点评 本题考查了圆的切线方程,考查了点到直线的距离公式的应用,是中档题.


科目:高中数学 来源: 题型:解答题
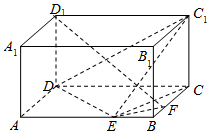 如图,在长方体ABCD-A1B1C1D1中,已知AB=4,AD=3,AA1=2.E、F分别是线段AB、BC上的点,且EB=FB=1.
如图,在长方体ABCD-A1B1C1D1中,已知AB=4,AD=3,AA1=2.E、F分别是线段AB、BC上的点,且EB=FB=1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $cos(2x-\frac{π}{6})$ | B. | $sin(2x-\frac{π}{6})$ | C. | $cos(2x-\frac{π}{3})$ | D. | $sin(2x-\frac{π}{3})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向右平移$\frac{π}{12}$个单位 | B. | 向左平移$\frac{π}{4}$个单位 | ||
| C. | 向左平移$\frac{π}{12}$个单位 | D. | 向右平移$\frac{π}{4}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
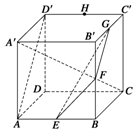 在正方体ABCD-A′B′C′D′中,棱AB,BB′,B′C′,C′D′的中点分别是E,F,G,H,如图所示.
在正方体ABCD-A′B′C′D′中,棱AB,BB′,B′C′,C′D′的中点分别是E,F,G,H,如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com