Question

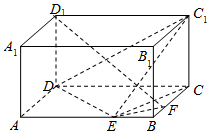
16．如图，在长方体ABCD-A₁B₁C₁D₁中，已知AB=4，AD=3，AA₁=2．E、F分别是线段AB、BC上的点，且EB=FB=1．
（1）求直线EC₁与FD₁所成角的余弦值；
（2）求二面角C-DE-C₁的平面角的余弦值．

Answer 1

分析 （1）以A为原点，AB、AD、AA₁所在直线分别为x轴，y轴，z轴，建立空间直角坐标系A-xyz，利用向量法能求出直线EC₁与FD₁所成角的余弦值．
（2）求出平面C₁DE的法向量和平面CDE的一个法向量，利用向量法能求出二面角C-DE-C₁的平面角的余弦值．

解答 解：（1）以A为原点，AB、AD、AA₁所在直线分别为x轴，y轴，z轴，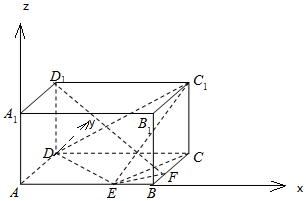
建立空间直角坐标系A-xyz，
则有D（0，3，0），D₁（0，3，2），E（3，0，0），F（4，1，0），C₁（4，3，2）．
∴$\overrightarrow{E{C}_{1}}$=（1，3，2），$\overrightarrow{F{D}_{1}}$=（-4，2，2）．
设EC₁与FD₁所成角为β，
则cosβ=|$\frac{\overrightarrow{E{C}_{1}}•\overrightarrow{F{D}_{1}}}{|E{C}_{1}|•|\overrightarrow{F{D}_{1}}|}$=|$\frac{1×（-4）+3×2+2×2}{\sqrt{14}•\sqrt{24}}$|=$\frac{\sqrt{21}}{14}$． 
∴直线EC₁与FD₁所成角的余弦值为$\frac{\sqrt{21}}{14}$．…（6分）
（2）设向量$\overrightarrow{n}$=（x，y，z）为平面C₁DE的法向量，
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{DE}=3x-3y=0}\\{\overrightarrow{n}•\overrightarrow{E{C}_{1}}=x+3y+2z=0}\end{array}\right.$，取z=2，则$\overrightarrow{n}$=（-1，-1，2）．
又向量$\overrightarrow{A{A}_{1}}$=（0，0，2）是平面CDE的一个法向量．
设二面角C-DE-C₁的平面角的为θ，
∴cosθ=$\frac{|\overrightarrow{n}•\overrightarrow{A{A}_{1}}|}{|\overrightarrow{n}|•|\overrightarrow{A{A}_{1}}|}$=$\frac{4}{\sqrt{6}•2}=\frac{\sqrt{6}}{3}$．             …（12分）
又二面角C-DE-C₁的平面角为锐角，
∴二面角C-DE-C₁的平面角的余弦值为$\frac{\sqrt{6}}{3}$．…（14分）

点评 本题考查线面角、二面角的余弦值的求法，考查几何体的体积的求法，涉及到空间中线线、线面、面面间的位置关系等基础知识，考查推理论证能力、运算求解能力、空间想象能力，考查化归与转化思想，是中档题．