
 如图所示,一辆汽车从O点出发沿一条直线公路以50千米/时的速度匀速行驶(图中的箭头方向为汽车行驶方向),汽车开动的同时,在距汽车出发点O点的距离为5千米、距离公路线的垂直距离为3千米的M点的地方有一个人骑摩托车出发想把一件东西送给汽车司机,问骑摩托车的人至少以多大的速度匀速行驶才能实现他的愿望,此时他驾驶摩托车行驶了多少千米?
如图所示,一辆汽车从O点出发沿一条直线公路以50千米/时的速度匀速行驶(图中的箭头方向为汽车行驶方向),汽车开动的同时,在距汽车出发点O点的距离为5千米、距离公路线的垂直距离为3千米的M点的地方有一个人骑摩托车出发想把一件东西送给汽车司机,问骑摩托车的人至少以多大的速度匀速行驶才能实现他的愿望,此时他驾驶摩托车行驶了多少千米? 分析 设在A处追上汽车,速度为v,时间为t,用余弦定理表示出AM,得出v关于t的函数,得出v的最小值及其成立的条件.
解答 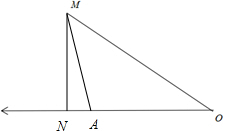 解:过M作公路的垂线MN,垂足为N,OM=5,MN=3,
解:过M作公路的垂线MN,垂足为N,OM=5,MN=3,
∴sin∠MON=$\frac{MN}{OM}$=$\frac{3}{5}$,cos∠MON=$\frac{4}{5}$,ON=4.
设骑摩托车的人的速度为v公里/小时,经过t小时后在A处追上汽车,则OA=50t,
在△MOA中,由余弦定理得AM2=25+2500t2-2×$5×50t×\frac{4}{5}$
=2500t2-400t+25,
又AM=vt,
∴v2t2=2500t2-400t+25,即v2=$\frac{25}{{t}^{2}}$-$\frac{400}{t}$+2500=25($\frac{1}{t}$-8)2+900≥900,
∴当t=$\frac{1}{8}$时,V取得最小值30,此时,AM=vt=$\frac{15}{4}$.
故骑摩托车的人至少以30公里/时的速度行驶才能实现他的愿望,他驾驶摩托车行驶了$\frac{15}{4}$公里.
点评 本题主要考查二次函数的性质,余弦定理的应用,属于中档题.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
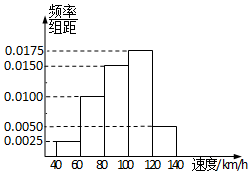 根据某固定测速点测得的某时段内过往的200辆机动车的行驶速度(单位:km/h)绘制的频率分布直方图如图所示.该路段限速标志牌提示机动车辆正常行驶速度为60km/h-120km/h,则该时段内非正常行驶的机动车辆数为30.
根据某固定测速点测得的某时段内过往的200辆机动车的行驶速度(单位:km/h)绘制的频率分布直方图如图所示.该路段限速标志牌提示机动车辆正常行驶速度为60km/h-120km/h,则该时段内非正常行驶的机动车辆数为30.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
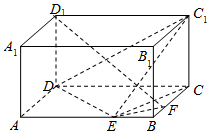 如图,在长方体ABCD-A1B1C1D1中,已知AB=4,AD=3,AA1=2.E、F分别是线段AB、BC上的点,且EB=FB=1.
如图,在长方体ABCD-A1B1C1D1中,已知AB=4,AD=3,AA1=2.E、F分别是线段AB、BC上的点,且EB=FB=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向右平移$\frac{π}{12}$个单位 | B. | 向左平移$\frac{π}{4}$个单位 | ||
| C. | 向左平移$\frac{π}{12}$个单位 | D. | 向右平移$\frac{π}{4}$个单位 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com