
分析 (1)求出f(x)的导数,通过讨论a的范围求出函数的单调区间即可;
(2)用x1表示x2,a,求出g(x1)-g(x2)的表达式,构造函数h(x)=(x-$\frac{1}{x}$)-(x+$\frac{1}{x}$)lnx,x∈(0,e],求出h(x)的最小值即可.
解答 解:(1)f(x)的定义域(0,+∞),
f′(x)=1+$\frac{1}{{x}^{2}}$-$\frac{a}{x}$=$\frac{{x}^{2}-ax+1}{{x}^{2}}$,
令f′(x)=0,得x2-ax+1=0,
①当0<a≤2时,△=a2-4≤0,此时f′(x)≥0恒成立,
∴f(x)在定义域(0,+∞)上单调递增;
②当a>2时,△=a2-4>0,x2-ax+1=0的两根为:
x1=$\frac{a-\sqrt{{a}^{2}-4}}{2}$,x2=$\frac{a+\sqrt{{a}^{2}-4}}{2}$,且x1,x2>0.
当x∈(0,$\frac{a-\sqrt{{a}^{2}-4}}{2}$)时,f′(x)>0,f(x)单调递增;
当x∈( $\frac{a-\sqrt{{a}^{2}-4}}{2}$,$\frac{a+\sqrt{{a}^{2}-4}}{2}$)时,f′(x)<0,f(x)单调递减;
当x∈( $\frac{a+\sqrt{{a}^{2}-4}}{2}$,+∞)时,f′(x)>0,f(x)单调递增;
综上,当0<a≤2时,f(x)的递增区间为(0,+∞),无递减区间;
当a>2时,f(x)的递增区间为(0,$\frac{a-\sqrt{{a}^{2}-4}}{2}$),( $\frac{a+\sqrt{{a}^{2}-4}}{2}$,+∞),
递减区间为( $\frac{a-\sqrt{{a}^{2}-4}}{2}$,$\frac{a+\sqrt{{a}^{2}-4}}{2}$).
(2)由(1)知,f(x)的两个极值点x1,x2是方程x2-ax+1=0的两个根,
则 $\left\{\begin{array}{l}{{x}_{1}{+x}_{2}=a}\\{{x}_{1}{•x}_{2}=1}\end{array}\right.$,所以x2=$\frac{1}{{x}_{1}}$,a=(x1+$\frac{1}{{x}_{1}}$),
∴g(x1)-g(x2)=x1-$\frac{a}{2}$lnx1-($\frac{1}{{x}_{1}}$-$\frac{a}{2}$ln$\frac{1}{{x}_{1}}$)
=x1-$\frac{1}{{x}_{1}}$-alnx1=x1-$\frac{1}{{x}_{1}}$-(x1+$\frac{1}{{x}_{1}}$)lnx1.
设h(x)=(x-$\frac{1}{x}$)-(x+$\frac{1}{x}$)lnx,x∈(0,e],
则(g(x1)-g(x2))min=h(x)min,
∵h′(x)=(1+$\frac{1}{{x}^{2}}$)-[(1-$\frac{1}{{x}^{2}}$)lnx+(x+$\frac{1}{x}$)$\frac{1}{x}$]=$\frac{(1+x)(1-x)lnx}{{x}^{2}}$,
当x∈(0,e]时,恒有h′(x)≤0,∴h(x)在(0,e]上单调递减;
∴h(x)min=h(e)=-$\frac{2}{e}$,
∴(g(x1)-g(x2))min=-$\frac{2}{e}$.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及函数的极值的意义,是一道综合题.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:选择题
| A. | 2ln2 | B. | ln2+1 | C. | ln2 | D. | ln2-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,渔船甲位于岛屿A的南偏西60°方向的B处,且与岛屿A相距6海里,渔船乙以5 海里/小时的速度从岛屿A出发沿正北方向航行,若渔船甲同时从B处出发沿北偏东α的方向追赶渔船乙,刚好用2小时追上.
如图,渔船甲位于岛屿A的南偏西60°方向的B处,且与岛屿A相距6海里,渔船乙以5 海里/小时的速度从岛屿A出发沿正北方向航行,若渔船甲同时从B处出发沿北偏东α的方向追赶渔船乙,刚好用2小时追上.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
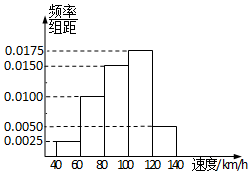 根据某固定测速点测得的某时段内过往的200辆机动车的行驶速度(单位:km/h)绘制的频率分布直方图如图所示.该路段限速标志牌提示机动车辆正常行驶速度为60km/h-120km/h,则该时段内非正常行驶的机动车辆数为30.
根据某固定测速点测得的某时段内过往的200辆机动车的行驶速度(单位:km/h)绘制的频率分布直方图如图所示.该路段限速标志牌提示机动车辆正常行驶速度为60km/h-120km/h,则该时段内非正常行驶的机动车辆数为30.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
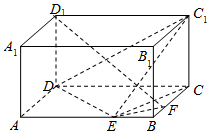 如图,在长方体ABCD-A1B1C1D1中,已知AB=4,AD=3,AA1=2.E、F分别是线段AB、BC上的点,且EB=FB=1.
如图,在长方体ABCD-A1B1C1D1中,已知AB=4,AD=3,AA1=2.E、F分别是线段AB、BC上的点,且EB=FB=1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com