
如图,储油灌的表面积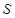 为定值,它的上部是半球,下部是圆柱,半球的半径等于圆柱底面半径.
为定值,它的上部是半球,下部是圆柱,半球的半径等于圆柱底面半径.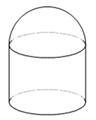
⑴试用半径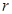 表示出储油灌的容积
表示出储油灌的容积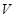 ,并写出
,并写出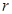 的范围.
的范围.
⑵当圆柱高 与半径
与半径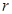 的比为多少时,储油灌的容积
的比为多少时,储油灌的容积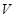 最大?
最大?
(1) (2)
(2)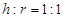
解析试题分析:(1)解决应用题问题首先要解决阅读问题,具体说就是要会用数学式子正确表示数量关系,本题先利用储油灌的表面积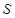 为定值得到圆柱高与半径的关系
为定值得到圆柱高与半径的关系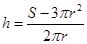 ,再根据储油灌的容积为半球体积与圆柱体积之和,即可得储油灌的容积
,再根据储油灌的容积为半球体积与圆柱体积之和,即可得储油灌的容积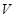 的解析式;为使思路简洁,直接用对应公式表示,根据高及半径为正数可得
的解析式;为使思路简洁,直接用对应公式表示,根据高及半径为正数可得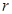 的取值范围,(2)本题解题思路清晰,就是利用导数求最值.难点在运算上,需用字母
的取值范围,(2)本题解题思路清晰,就是利用导数求最值.难点在运算上,需用字母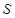 表示高
表示高 与半径
与半径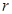 .由导数为零得
.由导数为零得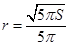 ,又由(1)得
,又由(1)得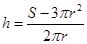 代入化简得
代入化简得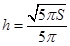 ,因此
,因此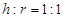 .
.
试题解析:⑴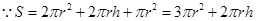 ,
,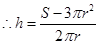 , 3分
, 3分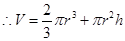
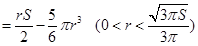 ; 7分
; 7分
⑵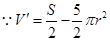 ,令
,令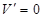 ,得
,得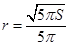 ,列表
,列表
11分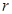
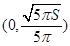
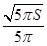
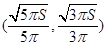
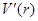
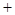
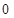
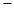
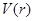
↗ 极大值即最大值 ↘
∴当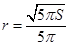 时,体积
时,体积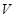 取得最大值,此时
取得最大值,此时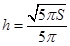 ,
,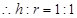 . 13分
. 13分
答:储油灌容积 ,当
,当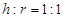 时容积
时容积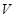 取得最大值. 15分
取得最大值. 15分
考点:圆柱侧面积,球的体积,利用导数求最值


科目:高中数学 来源: 题型:解答题
如图,四棱锥P ABCD中,PA⊥底面ABCD,PA=2
ABCD中,PA⊥底面ABCD,PA=2 ,BC="CD=2," ∠ACB=∠ACD=
,BC="CD=2," ∠ACB=∠ACD=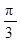 .
.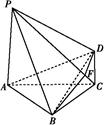
(1)求证:BD⊥平面PAC;
(2)若侧棱PC上的点F满足PF=7FC,求三棱锥P BDF的体积.
BDF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在三棱锥S ABC中,平面EFGH分别与BC,CA,AS,SB交于点E,F,G,H,且SA⊥平面EFGH,SA⊥AB,EF⊥FG.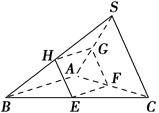
求证:(1)AB∥平面EFGH;
(2)GH∥EF;
(3)GH⊥平面SAC.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知一个四棱锥P-ABCD的三视图(正视图与侧视图为直角三角形,俯视图是带有一条对角线的正方形)如图,E是侧棱PC的中点.
(1)求四棱锥P-ABCD的体积;
(2)求证:平面APC⊥平面BDE.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在几何体ABCDE中,∠BAC=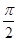 ,DC⊥平面ABC,EB⊥平面ABC, AB=AC=BE=2,CD=1。
,DC⊥平面ABC,EB⊥平面ABC, AB=AC=BE=2,CD=1。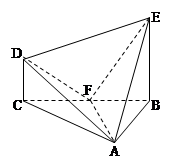
(1)设平面ABE与平面ACD的交线为直线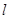 ,求证:
,求证: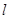 ∥平面BCDE;
∥平面BCDE;
(2)设F是BC的中点,求证:平面AFD⊥平面AFE;
(3)求几何体ABCDE的体积。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图C,D是以AB为直径的圆上的两点,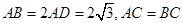 ,F是AB上的一点,且
,F是AB上的一点,且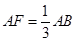 ,将圆沿AB折起,使点C在平面ABD的射影E在BD上,已知
,将圆沿AB折起,使点C在平面ABD的射影E在BD上,已知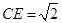
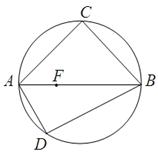
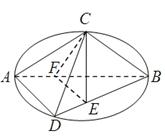
(1)求证:AD 平面BCE
平面BCE
(2)求证:AD//平面CEF;
(3)求三棱锥A-CFD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,四边形ABCD为矩形,四边形ADEF为梯形,AD//FE,∠AFE=60º,且平面ABCD⊥平面ADEF,AF=FE=AB= =2,点G为AC的中点.
=2,点G为AC的中点.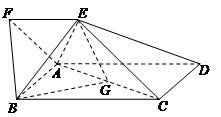
(Ⅰ)求证:EG//平面ABF;
(Ⅱ)求三棱锥B-AEG的体积;
(Ⅲ)试判断平面BAE与平面DCE是否垂直?若垂直,请证明;若不垂直,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,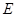 是以
是以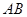 为直径的半圆上异于点
为直径的半圆上异于点 的点,矩形
的点,矩形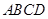 所在的平面垂直于该半圆所在平面,且
所在的平面垂直于该半圆所在平面,且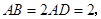
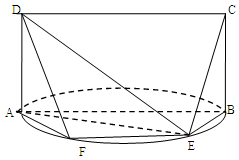
(Ⅰ)求证: ;
;
(Ⅱ)设平面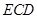 与半圆弧的另一个交点为
与半圆弧的另一个交点为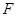 ,
,
①求证: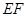 //
//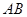 ;
;
②若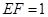 ,求三棱锥E-ADF的体积.
,求三棱锥E-ADF的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com