
| A. | [-$\frac{π}{2}$+2kπ,π+2kπ],k∈Z | B. | [-$\frac{π}{2}$+3kπ,π+3kπ],k∈Z | ||
| C. | [π+2kπ,$\frac{5π}{2}$+2kπ],k∈Z | D. | [π+3kπ,$\frac{5π}{2}$+3kπ],k∈Z |
分析 根据f(a)=-$\frac{1}{2}$,f(β)=$\frac{1}{2}$求出α、β的值,再根据|α-β|的最小值求出ω的值,
写出f(x)的解析式,从而求出f(x)的单调增区间.
解答 解:函数f(x)=sin(ωx-$\frac{π}{6}$)+$\frac{1}{2}$(ω>0),且f(a)=-$\frac{1}{2}$,f(β)=$\frac{1}{2}$,
∴f(α)=sin(ωα-$\frac{π}{6}$)+$\frac{1}{2}$=-$\frac{1}{2}$,可得ωα-$\frac{π}{6}$=2k1π-$\frac{π}{2}$,k1∈Z,
解得:α=$\frac{{2k}_{1}π-\frac{π}{3}}{ω}$,k1∈Z;
f(β)=sin(ωβ-$\frac{π}{6}$)+$\frac{1}{2}$=$\frac{1}{2}$,可得ωβ-$\frac{π}{6}$=k2π,k2∈Z,
解得:β=$\frac{{k}_{2}π+\frac{π}{6}}{ω}$,k2∈Z;
∵|α-β|的最小值为$\frac{3π}{4}$,
∴|α-β|=|$\frac{{2k}_{1}π{-k}_{2}π-\frac{π}{2}}{ω}$|=$\frac{π}{ω}$|2k1-k2-$\frac{1}{2}$|≥$\frac{3π}{4}$,k1∈Z,k2∈Z,
可解得:ω≤$\frac{4}{3}$|2k1-k2-$\frac{1}{2}$|,k1∈Z,k2∈Z,
取k1=1.k2=2,可得ω=$\frac{2}{3}$;
∴f(x)=sin($\frac{2}{3}$x-$\frac{π}{6}$)+$\frac{1}{2}$,
由2kπ-$\frac{π}{2}$≤$\frac{2}{3}$x-$\frac{π}{6}$≤2kπ+$\frac{π}{2}$,k∈Z,
解得3kπ-$\frac{π}{2}$≤x≤3kπ+π,k∈Z;
∴函数f(x)的单调递增区间为:[3kπ-$\frac{π}{2}$,3kπ+π],k∈Z.
故选:B.
点评 本题主要考查了正弦函数的图象与性质的应用问题,也考查了分析问题解答问题的能力,是综合性题目.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c>b>a | B. | b>c>a | C. | a>b>c | D. | c>a>b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2015-2016学年河北省保定市高一上学期期中考试数学试卷(解析版) 题型:选择题
函数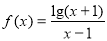 的定义域是( )
的定义域是( )
A.(﹣1,+∞) B.[﹣1,+∞)
C.(﹣1,1)∪(1,+∞) D.[﹣1,1)∪(1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某加油站工作人员根据以往该加油站的销售情况,绘制了该加油站日销售量的频率分布直方图,如图所示.将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.
某加油站工作人员根据以往该加油站的销售情况,绘制了该加油站日销售量的频率分布直方图,如图所示.将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com