
分析 an是与$\sqrt{n}$(n∈N*)最接近的正整数,可得:n=1,2时,an=1;n=3,4,5,6时,an=2;n=7,8,…,12时,an=3;…n=91,92,…,100时,an=10.即可得出.
解答 解:∵an是与$\sqrt{n}$(n∈N*)最接近的正整数,
∴n=1,2时,an=1;
n=3,4,5,6时,an=2;
n=7,8,…,12时,an=3;
n=13,14,…,20时,an=4;
n=21,14,…,30时,an=5;
n=31,32,…,40,41,42时,an=6;
n=43,44,…,56时,an=7;
n=57,59,…,72时,an=8;
n=73,74,…,90时,an=9;
n=91,92,…,100时,an=10.
∴$\sum_{i=1}^{100}$$\frac{1}{{a}_{i}}$=2+$4×\frac{1}{2}$+$6×\frac{1}{3}$+$8×\frac{1}{4}$+$10×\frac{1}{5}$+$12×\frac{1}{6}$+$14×\frac{1}{7}$+16×$\frac{1}{8}$+18×$\frac{1}{9}$+10×$\frac{1}{10}$=19.
故答案为:19.
点评 本题考查了数列递推关系、分类讨论方法、整数的性质,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
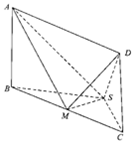 如图,在四棱锥S-ABCD中,底面ABCD是矩形,平面ABCD⊥平面SBC,SB=SC,M是BC的中点,AB=1,BC=2.
如图,在四棱锥S-ABCD中,底面ABCD是矩形,平面ABCD⊥平面SBC,SB=SC,M是BC的中点,AB=1,BC=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
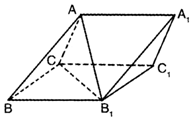 如图,三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,AC=AB1.
如图,三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,AC=AB1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),其导函数的图象f'(x)如图所示,则$f({\frac{π}{2}})$的值为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),其导函数的图象f'(x)如图所示,则$f({\frac{π}{2}})$的值为( )| A. | $2\sqrt{3}$ | B. | 2 | C. | $2\sqrt{2}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | -1 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com