
分析 由于直线过定点M(3,1),点M在圆C:(x-1)2+(y-2)2=25的内部,故直线被圆截得的弦长最短时,CM垂直于直线l,即可得出结论.
解答 解:直线l:(2m+1)x+(m+1)y-7m-4=0 即(x+y-4)+m(2x+y-7)=0,过定点M(3,1),
由于点M在圆C:(x-1)2+(y-2)2=25的内部,故直线被圆截得的弦长最短时,CM垂直于直线l,CM=$\sqrt{(3-1)^{2}+(1-2)^{2}}$=$\sqrt{5}$
l被圆C截得的最短弦长为2$\sqrt{25-5}$=4$\sqrt{5}$,
故答案为:4$\sqrt{5}$.
点评 本题主要考查直线和圆的位置关系,直线过定点问题,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
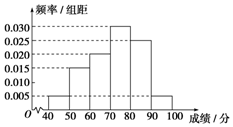 某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩(均为整数)的频率分布直方图如图,估计这次测试中数学成绩的平均分、众数、中位数分别是( )
某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩(均为整数)的频率分布直方图如图,估计这次测试中数学成绩的平均分、众数、中位数分别是( )| A. | 73.3,75,72 | B. | 72,75,73.3 | C. | 75,72,73.3 | D. | 75,73.3,72 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $4\sqrt{2}$ | C. | 6 | D. | $2\sqrt{10}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com