
分析 利用辅助角公式,结合三角函数的图象和性质即可得到结论.
解答 解:设y=2sinx+$\sqrt{5}$cosx,
则y=3($sinx•\frac{2}{3}+cosx•\frac{\sqrt{5}}{3}$)=3sin(x+θ),(tanθ=$\frac{\sqrt{5}}{2}$),
则-3≤y≤3,
若方程2sinx+$\sqrt{5}$cosx=$\frac{1}{k}$有解,
则-3≤$\frac{1}{k}$≤3,
解得k≥$\frac{1}{3}$或k≤-$\frac{1}{3}$,
即实数k的范围是k≥$\frac{1}{3}$或k≤-$\frac{1}{3}$.
点评 本题主要考查三角函数的图象和性质,利用辅助角公式将函数进行化简,求出函数的最值是解决本题的关键.


科目:高中数学 来源:2017届江西省红色七校高三上学期联考一数学(文)试卷(解析版) 题型:解答题
如图,已知直三棱柱 中,
中, ,
,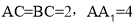 ,
, 是棱
是棱 上的一点,
上的一点, 分别为
分别为 的中点.
的中点.
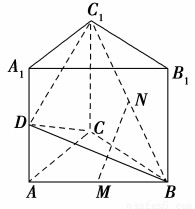
(1)求证: ∥平面
∥平面 ;
;
(2)当 为
为 的中点时,求三棱锥
的中点时,求三棱锥 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源:2017届河北正定中学高三上月考一数学(理)试卷(解析版) 题型:解答题
已知函数 ,且
,且 .
.
(1)若函数 在区间
在区间 上是减函数,求实数
上是减函数,求实数 的取值范围;
的取值范围;
(2)设函数 ,当
,当 时,
时, 恒成立,求
恒成立,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知顶点在原点、焦点F在y轴正半轴上的抛物线C1过点(2,1),抛物线C2与C1关于x轴对称.
已知顶点在原点、焦点F在y轴正半轴上的抛物线C1过点(2,1),抛物线C2与C1关于x轴对称.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4π | B. | 8π | C. | 16π | D. | 24π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 两个分类变量关系较弱 | B. | 两个分类变量无关系 | ||
| C. | 两个分类变量关系较强 | D. | 无法判断 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com