
分析 (1)按照一元二次不等式的解法容易获解;
(2)结合二次函数的性质可知,开口向上,对称轴x=1,因此只需最小值f(1)大于等于0即可.
解答 解:(1)由题意得f(x)=x2-2x-1,令f(x)=0得$x=1±\sqrt{2}$.
所以f(x)<0的解集为:{x|$1-\sqrt{2}<x<1+\sqrt{2}$}.
(2)由题意x2-2x+a≥0在(0,+∞)上恒成立.
因为函数f(x)开口向上,且对称轴x=1,所以当x∈(0,+∞)时,f(x)最小值为f(1)=a-1,
由题意只需a-1≥0即可,即a≥1.
故所求a的范围是[1,+∞).
点评 本题考查了一元二次不等式的解法以及不等式恒成立问题转化为函数最值问题来解的基本思路,难度不大.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:高中数学 来源:2017届山东潍坊临朐县高三10月月考数学(文)试卷(解析版) 题型:选择题
对于正整数 ,若数列
,若数列 为等差数列,则
为等差数列,则 是
是 的( )
的( )
A.必要不充分条件 B.充分不必要条件
C.充分必要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2017届江西省红色七校高三上学期联考一数学(理)试卷(解析版) 题型:选择题
把复数 的共轭复数记作
的共轭复数记作 ,已知
,已知 ,(其中i为虚数单位),则复数
,(其中i为虚数单位),则复数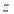 在坐标平面内对应的点在( )
在坐标平面内对应的点在( )
A.第四象限 B.第三象限 C.第二象限 D.第一象限
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com