
求二项式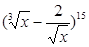 的展开式中:
的展开式中:
(1)常数项(答案可保留组合数);(2)有几个有理项;(3)有几个整式项.
科目:高中数学 来源: 题型:解答题
规定 ,其中
,其中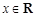 ,
, 为正整数,且
为正整数,且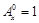 ,这是排列数
,这是排列数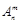 (
( 是正整数,且
是正整数,且 )的一种推广.
)的一种推广.
(1)求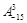 的值;
的值;
(2)排列数的两个性质:①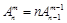 ,②
,②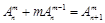 (其中
(其中 是正整数).是否都能推广到
是正整数).是否都能推广到 (
(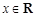 ,m是正整数)的情形?若能推广,写出推广的形式并给予证明;若不能,则说明理由;
,m是正整数)的情形?若能推广,写出推广的形式并给予证明;若不能,则说明理由;
(3)确定函数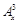 的单调区间.
的单调区间.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分14分)
在医学生物学试验中,经常以果蝇作为试验对象.一个关有6只果蝇的笼子里,不慎混入了两只苍蝇(此时笼内共有8只蝇子:6只果蝇和2只苍蝇),只好把笼子打开一个小孔,让蝇子一只一只地往外飞,直到两只苍蝇都飞出,再关闭小孔.
(Ⅰ)求笼内恰好剩下1只果蝇的概率;
(Ⅱ)求笼内至少剩下5只果蝇的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com