
分析 (1)利用函数的导数,f′(1)=0,求得a的值;
(2)令f′(x)=0,求出函数的极值点,根据导函数的正负判断函数的单调性,求得函数f(x)的单调区间.
解答 解:(1)f(x)=2x3+ax2+6,f′(x)=6x2+2ax,
由f(x)在x=1时取得极值,即f′(1)=0,
∴6+2a=0,
∴a=-3,
(2)f(x)=2x3-3x2+6,f′(x)=6x2-6x,
令f′(x)=0,解得:x=0或x=1,
当f′(x)>0,解得:x>1或x<0,
当f′(x)<0,解得:0<x<1,
当x变化时,f′(x),f(x)的变化情况如下表:
| x | (-∞,0) | 0 | (0,1) | 1 | (1,+∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | ↗ | 2 | ↘ | 1 | ↗ |
点评 本题考查函数的极值点以及函数的单调性的应用,考查利用导数研究函数单调与极值,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
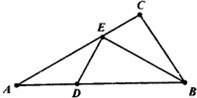 如图,在Rt△ABC中,∠C=90°,BE平分∠ABC,交AC于点E,过点E作ED⊥BE交AB于点D.
如图,在Rt△ABC中,∠C=90°,BE平分∠ABC,交AC于点E,过点E作ED⊥BE交AB于点D.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
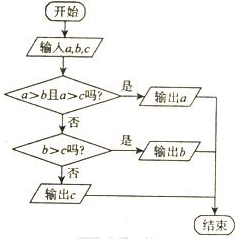 如图所示的流程图是将一系列指令和问题用框图的形式排列而成.箭头说明下一步是到哪一个框图,阅读这个流程图,回答下列问题:
如图所示的流程图是将一系列指令和问题用框图的形式排列而成.箭头说明下一步是到哪一个框图,阅读这个流程图,回答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 45° | B. | 90° | C. | 60° | D. | 30° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com