
| A. | λ$≥\frac{1}{3}$ | B. | λ$>\frac{1}{3}$ | C. | λ$≥\frac{4}{3}$ | D. | λ$>\frac{4}{3}$ |
分析 数列{an}满足:${a_1}=1,{a_{n+1}}=\frac{a_n}{{{a_n}+2}}(n∈N*)$,两边取倒数可得:$\frac{1}{{a}_{n+1}}$=$\frac{2}{{a}_{n}}$+1,变形为:$\frac{1}{{a}_{n+1}}$+1=2$(\frac{1}{{a}_{n}}+1)$,利用等比数列的通项公式可得$\frac{1}{{a}_{n}}$,代入${C_n}=(1+\frac{1}{a_n})(\frac{2}{n+1}-λ)$=2n$(\frac{2}{n+1}-λ)$.由于{Cn}是单调递减数列,可得cn+1<cn,化简整理,利用函数的单调性即可得出.
解答 解:∵数列{an}满足:${a_1}=1,{a_{n+1}}=\frac{a_n}{{{a_n}+2}}(n∈N*)$,
∴$\frac{1}{{a}_{n+1}}$=$\frac{2}{{a}_{n}}$+1,
变形为:$\frac{1}{{a}_{n+1}}$+1=2$(\frac{1}{{a}_{n}}+1)$,
∴数列$\{\frac{1}{{a}_{n}}+1\}$是等比数列,首项为2,公比为2.
∴$\frac{1}{{a}_{n}}$+1=2n,
∴${C_n}=(1+\frac{1}{a_n})(\frac{2}{n+1}-λ)$=2n$(\frac{2}{n+1}-λ)$,
∵{Cn}是单调递减数列,
∴cn+1<cn,
∴2n+1$(\frac{2}{n+2}-λ)$<2n$(\frac{2}{n+1}-λ)$,
化为:λ>$\frac{2n}{(n+1)(n+2)}$=$\frac{2}{n+\frac{2}{n}+3}$,
令f(x)=x+$\frac{2}{x}$+3,(x∈[1,+∞)).
f′(x)=1-$\frac{2}{{x}^{2}}$=$\frac{{x}^{2}-2}{{x}^{2}}$,可知当x≥$\sqrt{2}$时,单调递增;
而f(1)=6,f(2)=6,
∴f(x)的最小值为6,
因此$\frac{2}{n+\frac{2}{n}+3}$的最大值为$\frac{1}{3}$,
∴$λ>\frac{1}{3}$.
故选:B.
点评 本题考查了递推关系、函数与数列的单调性、单调性,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
| 积极参加团队活动 | 不太积极参加团队活动 | 合计 | |
| 工作积极性高 | 18 | 7 | 25 |
| 工作积极性不高 | 6 | 19 | 25 |
| 合计 | 24 | 26 | 50 |
| p(K2≥k0) | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{AB}•\overrightarrow{{A_1}C}=2{a^2}$ | B. | $\overrightarrow{AB}•\overrightarrow{AC}=\sqrt{2}{a^2}$ | C. | $\overrightarrow{AB}•\overrightarrow{{A_1}O}=\frac{1}{2}{a^2}$ | D. | $\overrightarrow{BC}•\overrightarrow{AO}={a^2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x-y+1=0或3x-2y=0 | B. | x-y+1=0 | ||
| C. | x+y-5=0或3x-2y=0 | D. | x+y-5=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
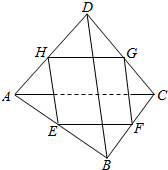 如图所示,在空间四边形ABCD中,E、F、G、H分别为AB、BC、CD、AD的中点,判断平面EG与直线BD是否平行?平面EG与直线AC是否平行?直线BD与直线AC是什么位置关系?
如图所示,在空间四边形ABCD中,E、F、G、H分别为AB、BC、CD、AD的中点,判断平面EG与直线BD是否平行?平面EG与直线AC是否平行?直线BD与直线AC是什么位置关系?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com