
| 积极参加团队活动 | 不太积极参加团队活动 | 合计 | |
| 工作积极性高 | 18 | 7 | 25 |
| 工作积极性不高 | 6 | 19 | 25 |
| 合计 | 24 | 26 | 50 |
| p(K2≥k0) | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 5.024 | 6.635 | 7.879 | 10.828 |
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
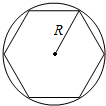 如图,半径为R的圆形纸板上有一内接正六边形图案,将一颗豆子随机地扔到平放的纸板上,假设豆子不落在线上,则豆子落在正六边形区域的概率是( )
如图,半径为R的圆形纸板上有一内接正六边形图案,将一颗豆子随机地扔到平放的纸板上,假设豆子不落在线上,则豆子落在正六边形区域的概率是( )| A. | $\frac{3}{2π}$ | B. | $\frac{3\sqrt{3}}{2π}$ | C. | $\frac{3}{4π}$ | D. | $\frac{3\sqrt{3}}{4π}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 必要而不充分条件 | B. | 充分而不必要条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | λ$≥\frac{1}{3}$ | B. | λ$>\frac{1}{3}$ | C. | λ$≥\frac{4}{3}$ | D. | λ$>\frac{4}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com