
分析 设P的坐标为P(m,n),得到$\overrightarrow{AP}$=(m-2,n-1),$\overrightarrow{AM}$=(x-2,y-1),然后根据$\overrightarrow{AP}$=2$\overrightarrow{AM}$,求出P点的坐标,进而代入抛物线方程即可得答案.
解答 解:设点P的坐标为(m,n),
则$\overrightarrow{AP}$=(m-2,n-1),$\overrightarrow{AM}$=(x-2,y-1),
∵$\overrightarrow{AP}$=2$\overrightarrow{AM}$,
∴m-2=2(x-2),n-1=2(y-1),
∴m=2x-2,n=2y-1,
即点P坐标为(2x-2,2y-1)
而点P在抛物线y2=2x上,
因此有(2y-1)2=2(2x-2),
即(y-$\frac{1}{2}$)2=x-1.
∴动点M的轨迹方程为(y-$\frac{1}{2}$)2=x-1.
点评 本题主要考查通过向量的有关运算求轨迹方程的问题.对向量的有关题型比如:求模、求夹角、求垂直以及平行等的问题一定要强化练习,是高考的热点问题.


 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 最大值3+4$\sqrt{3}$ | B. | 最小值3+4$\sqrt{3}$ | C. | 最大值3+2$\sqrt{3}$ | D. | 最小值3+2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
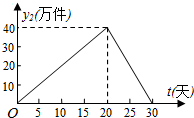 我市某外资企业生产的一批产品上市后30天内全部售完,该企业对这批产品上市后每天的销售情况进行了跟踪调查.其中,国内市场的日销售量y1(万件)与时间t(t为整数,单位:天)的部分对应值如下表所示.而国外市场的日销售量y2(万件)与时间t(t为整数,单位:天)的关系如图所示.
我市某外资企业生产的一批产品上市后30天内全部售完,该企业对这批产品上市后每天的销售情况进行了跟踪调查.其中,国内市场的日销售量y1(万件)与时间t(t为整数,单位:天)的部分对应值如下表所示.而国外市场的日销售量y2(万件)与时间t(t为整数,单位:天)的关系如图所示.| 时间t(天) | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
| 日销售量y1(万件) | 0 | 25 | 40 | 45 | 40 | 25 | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{S}_{6}}{{a}_{6}}$ | B. | $\frac{{S}_{7}}{{a}_{7}}$ | C. | $\frac{{S}_{9}}{{a}_{9}}$ | D. | $\frac{{S}_{8}}{{a}_{8}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 二次函数y=ax2+bx+c的图象如图所示,下列结论:a+b+c>0;②a-b+c>0;③abc<0;④2a-b=0,其中正确的个数是( )
二次函数y=ax2+bx+c的图象如图所示,下列结论:a+b+c>0;②a-b+c>0;③abc<0;④2a-b=0,其中正确的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com