
分析 求出函数的定义域关于原点对称,再化简函数,利用奇函数的定义进行判断即可.
解答 解:由题意,$\left\{\begin{array}{l}{1-{x}^{2}≥0}\\{2-|x+2|≠0}\end{array}\right.$,∴-1≤x≤1且x≠0,关于原点对称.
∴f(x)=$\frac{{\sqrt{1-{x^2}}}}{{2-\left|{x+2}\right|}}$=$\frac{\sqrt{1-{x}^{2}}}{-x}$,
∴f(-x)=-f(x),
∴函数f(x)=$\frac{{\sqrt{1-{x^2}}}}{{2-\left|{x+2}\right|}}$是奇函数,
故答案为:奇.
点评 本题考查函数奇偶性的判断,考查学生的计算能力,确定函数的定义域是关键.


科目:高中数学 来源: 题型:选择题
| A. | [2,3] | B. | [4,6] | C. | [-5,-3] | D. | [-6,-4] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $x{(\frac{1}{a})^{x-1}}$ | B. | ${(\frac{1}{a})^x}lna$ | C. | -a-xlna | D. | -xa-x-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 17 | B. | 16 | C. | 15 | D. | 14 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$+1 | B. | 4$\sqrt{2}$ | C. | 3+2$\sqrt{2}$ | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
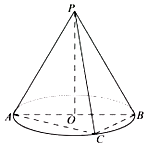 如图,设AB为圆锥PO的底面直径,PA为母线,点C在底面圆周上,若PA=AB=2,AC=BC,则二面角P-AC-B大小的正切值是( )
如图,设AB为圆锥PO的底面直径,PA为母线,点C在底面圆周上,若PA=AB=2,AC=BC,则二面角P-AC-B大小的正切值是( )| A. | $\frac{{\sqrt{6}}}{6}$ | B. | $\sqrt{6}$ | C. | $\frac{{\sqrt{7}}}{7}$ | D. | $\sqrt{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com