
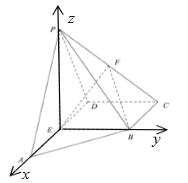
【题目】在四棱锥![]() 中,侧面
中,侧面![]() 底面ABCD,底面ABCD为直角梯形,
底面ABCD,底面ABCD为直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,E,F分别为AD,PC的中点.
,E,F分别为AD,PC的中点.

![]() Ⅰ
Ⅰ![]() 求证:
求证:![]() 平面BEF;
平面BEF;
![]() Ⅱ
Ⅱ![]() 若
若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2) ![]() .
.
【解析】
(1)连接![]() 交
交![]() 于
于![]() ,并连接
,并连接![]() ,
,![]() ,由空间几何关系可证得
,由空间几何关系可证得![]() ,利用线面平行的判断定理可得
,利用线面平行的判断定理可得![]() 平面
平面![]() .
.
(2)(法一)取![]() 中点
中点![]() ,连
,连![]() ,
,![]() ,
,![]() ,由二面角的定义结合几何体的特征可知
,由二面角的定义结合几何体的特征可知![]() 为二面角
为二面角![]() 的平面角,计算可得二面角
的平面角,计算可得二面角![]() 的余弦值为
的余弦值为![]() .
.
(法二)以![]() 为原点,
为原点,![]() 、
、![]() 、
、![]() 分别为
分别为![]() 、
、![]() 、
、![]() 建立直角坐标系,则平面
建立直角坐标系,则平面![]() 法向量可取:
法向量可取:![]() ,平面
,平面![]() 的法向量
的法向量![]() ,由空间向量的结论计算可得二面角
,由空间向量的结论计算可得二面角![]() 的余弦值为
的余弦值为![]() .
.
(1)连接![]() 交
交![]() 于
于![]() ,并连接
,并连接![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() 为
为![]() 中点,
中点, ![]() ,且
,且![]() ,
,
![]() 四边形
四边形![]() 为平行四边形,
为平行四边形,![]()
![]() 为
为![]() 中点,又
中点,又![]() 为
为![]() 中点,
中点,
![]()
![]() ,
, ![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
(2)(法一)由![]() 为正方形可得
为正方形可得![]() ,
,![]()
![]() .
.
取![]() 中点
中点![]() ,连
,连![]() ,
,![]() ,
,![]() ,
,![]() 侧面
侧面![]()
![]() 底面
底面![]() ,且交于
,且交于![]() ,
,![]()
![]()
![]() ,
,
![]() 面
面![]() ,又
,又![]() ,
,![]() 为二面角
为二面角![]() 的平面角,
的平面角,
又![]() ,
,![]() ,
,![]() ,
,
![]() ,所以二面角
,所以二面角![]() 的余弦值为
的余弦值为![]() .
.
(法二)由题意可知![]()
![]() 面
面![]() ,
,![]()
![]()
![]() ,如图所示,以
,如图所示,以![]() 为原点,
为原点,![]() 、
、![]() 、
、![]() 分别为
分别为![]() 、
、![]() 、
、![]() 建立直角坐标系,则
建立直角坐标系,则![]() ,
,![]() ,
,![]() ,
,![]() .
.
平面![]() 法向量可取:
法向量可取:![]() ,
,
平面![]() 中,设法向量为
中,设法向量为![]() ,则
,则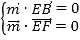
![]()
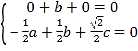 ,
,
取![]() ,
,
![]() ,所以二面角
,所以二面角![]() 的余弦值为
的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】某公司利用![]() 线上、实体店线下销售产品
线上、实体店线下销售产品![]() ,产品
,产品![]() 在上市
在上市![]() 天内全部售完.据统计,线上日销售量
天内全部售完.据统计,线上日销售量![]() 、线下日销售量
、线下日销售量![]() (单位:件)与上市时间
(单位:件)与上市时间![]()
![]() 天的关系满足:
天的关系满足:![]()
![]()
![]() ,产品
,产品![]() 每件的销售利润为
每件的销售利润为![]() (单位:元)(日销售量
(单位:元)(日销售量![]() 线上日销售量
线上日销售量![]() 线下日销售量).
线下日销售量).
(1)设该公司产品![]() 的日销售利润为
的日销售利润为![]() ,写出
,写出![]() 的函数解析式;
的函数解析式;
(2)产品![]() 上市的哪几天给该公司带来的日销售利润不低于
上市的哪几天给该公司带来的日销售利润不低于![]() 元?
元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用符号“![]() ”或“
”或“![]() ”填空:
”填空:
(1)设A为所有亚洲国家组成的集合,则中国______________A,美国__________A,印度____________A,英国_____________A;
(2)若![]() ,则-1_____________A;
,则-1_____________A;
(3)若![]() ,则3________________B;
,则3________________B;
(4)若![]() ,则8_______________C,9.1____________C.
,则8_______________C,9.1____________C.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解学生对食堂伙食的满意程度,组织学生给食堂打分(分数为整数,满分100分),从中随机抽取一个容量为![]() 的样本,发现所有数据均在
的样本,发现所有数据均在![]() 内.现将这些分数分成以下
内.现将这些分数分成以下![]() 组:
组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,并画出了样本的频率分布直方图,部分图形如图所示.观察图形,回答下列问题:
,并画出了样本的频率分布直方图,部分图形如图所示.观察图形,回答下列问题:
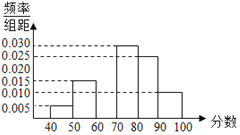
(1)算出第三组![]() 的频数,并补全频率分布直方图;
的频数,并补全频率分布直方图;
(2)请根据频率分布直方图,估计样本的众数和平均数,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市理论预测2014年到2018年人口总数![]() (单位:十万)与年份(用
(单位:十万)与年份(用![]() 表示)的关系如表所示:
表示)的关系如表所示:
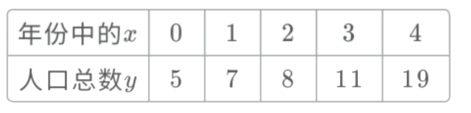
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的回归方程
的回归方程![]() ;
;
(3)据此估计2019年该城市人口总数.
(参考数据: ![]()
![]() )
)
参考公式:线性回归方程为![]() ,其中
,其中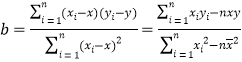 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的函数f(x)满足:如果对任意的x1,x2∈R,都有f(![]() )
)![]() ,则称函数f(x)是R上的凹函数,已知二次函数f(x)=ax2+x(a∈R,a≠0)
,则称函数f(x)是R上的凹函数,已知二次函数f(x)=ax2+x(a∈R,a≠0)
(1)当a=1,x∈[﹣2,2]时,求函数f(x)的值域;
(2)当a=1时,试判断函数f(x)是否为凹函数,并说明理由;
(3)如果函数f(x)对任意的x∈[0,1]时,都有|f(x)|≤1,试求实数a的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() ,(其中
,(其中![]() ,
, ![]() 为自然对数的底数,
为自然对数的底数, ![]() ……).
……).
(1)令![]() ,若
,若![]() 对任意的
对任意的![]() 恒成立,求实数
恒成立,求实数![]() 的值;
的值;
(2)在(1)的条件下,设![]() 为整数,且对于任意正整数
为整数,且对于任意正整数![]() ,
, ![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com