
分析 由题意作图,设点F1(-c,0)关于直线y=x+2的对称点为A(m,n),从而求出点A的坐标,从而结合题意得方程组,解之即可.
解答 解:由题意作图象如下,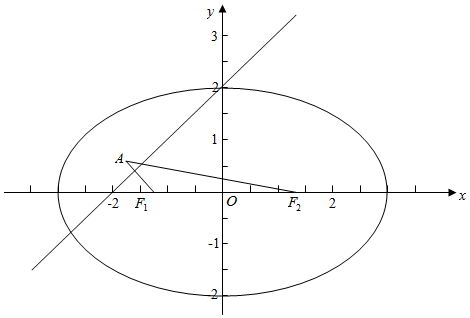 ,
,
设点F1(-c,0)关于直线y=x+2的对称点为A(m,n),
则$\left\{\begin{array}{l}{\frac{n-0}{m+c}=-1}\\{\frac{m-c}{2}-\frac{n}{2}+2=0}\end{array}\right.$,
解得,m=-2,n=2-c;
结合题意知,|AF2|=$\sqrt{10}$,
故可得方程组,
$\left\{\begin{array}{l}{e=\frac{c}{a}=\frac{\sqrt{3}}{3}}\\{{a}^{2}={b}^{2}+{c}^{2}}\\{\sqrt{(c+2)^{2}+(2-c)^{2}}=\sqrt{10}}\end{array}\right.$,
解得,c=1,a=$\sqrt{3}$,b=$\sqrt{2}$;
故椭圆的标准方程为$\frac{{x}^{2}}{3}$+$\frac{{y}^{2}}{2}$=1.
点评 本题考查了圆锥曲线与直线的位置关系的应用及数形结合的思想方法应用,同时考查了转化思想与方程思想.


科目:高中数学 来源: 题型:解答题
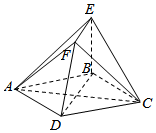 如图,四边形ABCD为菱形,EB⊥平面ABCD,EF∥BD,EF=$\frac{1}{2}$BD.
如图,四边形ABCD为菱形,EB⊥平面ABCD,EF∥BD,EF=$\frac{1}{2}$BD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
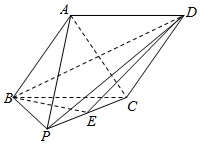 如图,在四棱锥P-ABCD中,底面ABCD是菱形,侧面PBC是直角三角形,∠PCB=90°,点E是PC的中点,且平面PBC⊥平面ABCD.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,侧面PBC是直角三角形,∠PCB=90°,点E是PC的中点,且平面PBC⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | ±i | C. | ±1 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
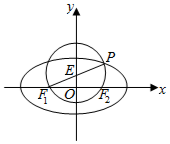 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)与圆E:x2+y2-y-2=0在第一象限相交于点P,椭圆C的左、右焦点F1,F2都在圆E上,且线段PF1为圆E的直径.
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)与圆E:x2+y2-y-2=0在第一象限相交于点P,椭圆C的左、右焦点F1,F2都在圆E上,且线段PF1为圆E的直径.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ±$\frac{4}{3}$ | B. | ±$\frac{3}{5}$ | C. | ±$\frac{3}{4}$ | D. | ±$\frac{5}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
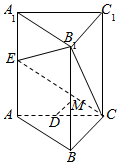 如图,直棱柱ABC-A1B1C1中,AB=AC=2,AA1=BC=2$\sqrt{3}$,E是AA1中点,D是AC的中点,M是BB1上一点,若DM∥平面B1CE,则$\frac{BM}{M{B}_{1}}$=3.
如图,直棱柱ABC-A1B1C1中,AB=AC=2,AA1=BC=2$\sqrt{3}$,E是AA1中点,D是AC的中点,M是BB1上一点,若DM∥平面B1CE,则$\frac{BM}{M{B}_{1}}$=3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com