
 如图,在正三棱柱ABC-A1B1C1中,AB=1,AA1=2,M是AB1上的动点,且AM=λAB1,N是CC1的中点.
如图,在正三棱柱ABC-A1B1C1中,AB=1,AA1=2,M是AB1上的动点,且AM=λAB1,N是CC1的中点.| 1 |
| 2 |
|
|
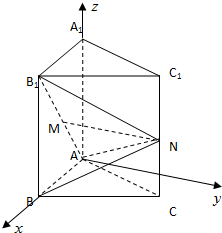 (Ⅰ)证明:取AB中点E,连结ME,CE,则有ME与NC平行且相等.
(Ⅰ)证明:取AB中点E,连结ME,CE,则有ME与NC平行且相等.| 1 |
| 2 |
| ||
| 2 |
| MN |
| 1 |
| 2 |
| ||
| 2 |
| AB |
| AN |
| 1 |
| 2 |
| ||
| 2 |
| n1 |
|
|
|
| n1 |
| ||
| 2 |
| MN |
| n1 |
| ||||||||||
|
|
| λ | ||||||
|
| 1 | ||
|
| 1 |
| 3 |
| 1 |
| 3 |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
 如图,多面体ABCC1A1B1中,四边形AA1C1C是正方形,四边形BCC1B1是直角梯形,CC1⊥BC且BC∥B1C1.△ACB、△A1C1B1都是等腰直角三角形,A、B1分别为直角顶点,M是B1B上的点,BM=2MB1.
如图,多面体ABCC1A1B1中,四边形AA1C1C是正方形,四边形BCC1B1是直角梯形,CC1⊥BC且BC∥B1C1.△ACB、△A1C1B1都是等腰直角三角形,A、B1分别为直角顶点,M是B1B上的点,BM=2MB1.查看答案和解析>>
科目:高中数学 来源: 题型:
 太阳岛公园引进了两种植物品种甲与乙,株数分别为18与12,这30株植物的株高编写成茎叶图如图(单位:cm):若这两种植物株高在185cm以上(包括185cm)定义为“优秀品种”,株高在185cm以下(不包括185cm)定义为“非优秀品种”.
太阳岛公园引进了两种植物品种甲与乙,株数分别为18与12,这30株植物的株高编写成茎叶图如图(单位:cm):若这两种植物株高在185cm以上(包括185cm)定义为“优秀品种”,株高在185cm以下(不包括185cm)定义为“非优秀品种”.查看答案和解析>>
科目:高中数学 来源: 题型:
| a1+a2+…+an |
| n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com