
分析 (1)将f(α)进行化简,将x=-$\frac{31π}{3}$带入计算即可;
(2)2f(π+α)=f($\frac{π}{2}$+α),建立等式关系,化简,利用弦化切的思想,即可求出$\frac{sinα+cosα}{sinα-cosα}$+cos2α的值.
(3)f(α)=$\frac{3}{5}$,建立等式关系,化简,根据同角三角函数关系式计算即可.
解答 解:由f(α)=$\frac{{sin({π-α})cos({2π-α})tan({-α+\frac{3π}{2}})}}{{cos({-π-α})}}$=$\frac{sinα•cosα×\frac{1}{tanα}}{-cosα}$=$\frac{co{s}^{2}α}{-cosα}=-cosα$.
(1)当x=-$\frac{31π}{3}$时,即f(-$\frac{31π}{3}$)=-cos($\frac{31π}{3}$)=-cos(10π+$\frac{π}{3}$)=-$\frac{1}{2}$.
(2)2f(π+α)=f($\frac{π}{2}$+α),即-2cos(π+α)=-cos($\frac{π}{2}+α$),
可得:2cosα=sinα,
∴tanα=2.
那么:$\frac{sinα+cosα}{sinα-cosα}$+cos2α=$\frac{tanα+1}{tanα-1}+\frac{co{s}^{2}α}{si{n}^{2}α+co{s}^{2}a}$=$\frac{2+1}{2-1}+\frac{1}{1+ta{n}^{2}α}$=$\frac{16}{5}$.
(3)∵f(α)=$\frac{3}{5}$,即-cosα=$\frac{3}{5}$,
∴cosα=$-\frac{3}{5}$.
那么:sinα=$±\sqrt{1-co{s}^{2}α}$=$±\frac{4}{5}$.
点评 本题主要考查三角函数的化简计算能力.属于基础题.


科目:高中数学 来源: 题型:选择题
 如图所示,正方体ABCD-A1B1C1D1的棱长为a,M,N分别为A1B和AC上的点,A1M=AN=$\frac{a}{3}$,则MN与平面BB1C1C的位置关系为( )
如图所示,正方体ABCD-A1B1C1D1的棱长为a,M,N分别为A1B和AC上的点,A1M=AN=$\frac{a}{3}$,则MN与平面BB1C1C的位置关系为( )| A. | 相交 | B. | 平行 | C. | 垂直 | D. | 不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
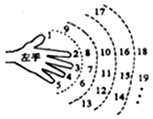 某小朋友按如下规则练习数数,1大拇指,2食指,3中指,4无名指,5小指,6无名指,7中指,8食指,9大拇指,10食指,…,一直数到2017时,对应的指头是大拇指.
某小朋友按如下规则练习数数,1大拇指,2食指,3中指,4无名指,5小指,6无名指,7中指,8食指,9大拇指,10食指,…,一直数到2017时,对应的指头是大拇指.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com