Question

18．已知函数f（x）=$\left\{{\begin{array}{l}{|{{{log}_2}x}|，\;0＜x≤4}\\{{x^2}-12x+34\;，x＞4}\end{array}}$，若方程f（x）=t，（t∈R）有四个不同的实数根x₁，x₂，x₃，x₄，则x₁x₂x₃x₄的取值范围为（32，34）．

Answer 1

分析 作函数f（x）=$\left\{{\begin{array}{l}{|{{{log}_2}x}|，\;0＜x≤4}\\{{x^2}-12x+34\;，x＞4}\end{array}}$的图象，从而可得x₁x₂=1，且x₃+x₄=12，（4＜x₃＜6-$\sqrt{2}$），从而解得．

解答 解：作函数f（x）=$\left\{{\begin{array}{l}{|{{{log}_2}x}|，\;0＜x≤4}\\{{x^2}-12x+34\;，x＞4}\end{array}}$的图象如下，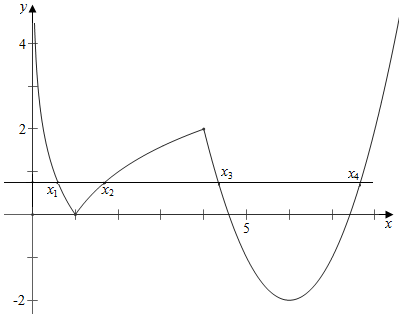
，
结合图象可知，-log₂x₁=log₂x₂，
故x₁x₂=1，
令x²-12x+34=0得，x=6±$\sqrt{2}$，
令x²-12x+34=2得，x=6±2；
故x₃+x₄=12，（4＜x₃＜6-$\sqrt{2}$），
故x₁x₂x₃x₄=x₃x₄
=x₃（12-x₃）
=-（x₃-6）²+36，
∵4＜x₃＜6-$\sqrt{2}$，
∴-2＜x₃-6＜-$\sqrt{2}$，
∴32＜-（x₃-6）²+36＜34，
故答案为：（32，34）．

点评 本题考查了数形结合的思想应用及学生的作图能力，同时考查了配方法的应用．