
| ʳ������ | �� | �� | �� |
| ά����C����λ/kg�� | 300 | 500 | 300 |
| ά����D����λ/kg�� | 700 | 100 | 300 |
| �ɱ���Ԫ/kg�� | 5 | 4 | 3 |
���� ��1������������������ʽ��ϵ������������Ӧ��ƽ������
��2���������Թ滮��Ӧ�ý���ƽ����⼴�ɣ�
���  �⣺�� I����Ϊx��0��y��0��
�⣺�� I����Ϊx��0��y��0��
��$\left\{\begin{array}{l}300x+500y+300��100-x-y����35000\\ 700x+100y+300��100-x-y����40000\end{array}\right.$��
����Ϊ$\left\{\begin{array}{l}y��25\\ 2x-y��50\end{array}\right.$��
���100-x-y��0��
���г�x��y�������ѧ��ϵʽΪ$\left\{\begin{array}{l}y��25\\ 2x-y��50\\ x+y��100\end{array}\right.$��
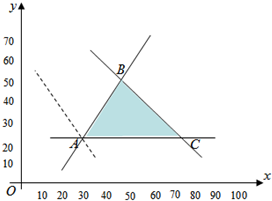
��xOyƽ���У�������Ӧ��ƽ��������ͼ��ʾ������7�֣�
�� II����100kg���ʳ��ijɱ�z=5x+4y+3��100-x-y��=2x+y+300��ƽ��������һ������������
����ΪA��37.5��25����B��50��50����C��75��25����
Ŀ�꺯��z=2x+y+300�ھ�����A��37.5��25��ʱ��zȡ����Сֵ400Ԫ������13�֣�
���� ������Ҫ�������Թ滮��Ӧ�����⣬����������������ʽ��ϵ��������Թ滮��֪ʶ��������ǽ������Ĺؼ����ۺ��Խ�ǿ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | i | B�� | -i | C�� | 1 | D�� | -1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֶ�����Ҫ���� | B�� | ��Ҫ����������� | ||
| C�� | ��ֱ�Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
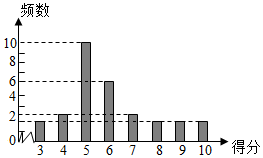 Ϊ���ռ�����֪ʶ����ǿ������ʶ�������ȡij��ѧ30��ѧ���μӻ���֪ʶ���ԣ��÷֣�10���ƣ���ͼ��ʾ������÷ֵ���λ��Ϊme������Ϊm����ƽ����Ϊ$\overline{x}$����me��m����$\overline{x}$֮��Ĵ�С��ϵ��m����me��$\overline{x}$��
Ϊ���ռ�����֪ʶ����ǿ������ʶ�������ȡij��ѧ30��ѧ���μӻ���֪ʶ���ԣ��÷֣�10���ƣ���ͼ��ʾ������÷ֵ���λ��Ϊme������Ϊm����ƽ����Ϊ$\overline{x}$����me��m����$\overline{x}$֮��Ĵ�С��ϵ��m����me��$\overline{x}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֲ���Ҫ���� | B�� | ��Ҫ��������� | ||
| C�� | ����ұ�Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -2 | B�� | 0 | C�� | 2 | D�� | 1-i |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��x2+x-2��0���ǡ�x��l���ij�ֲ���Ҫ���� | |
| B�� | ����am2��bm2����a��b��������������� | |
| C�� | ���⡰?x��R��ʹ��2x2-1��0���ķ��ǣ���?x��R������2x2-1��0�� | |
| D�� | ���⡰��x=$\frac{��}{4}$����tanx=1��������Ϊ������ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com