
分析 由互为逆否命题的两个命题共真假判断(1);
利用柯西不等式求得a2+4b2+9c2的最小值判断(2);
根据回归分析的定义可判断(3);
在三角形中,由a+b>c,得a+b-c>0,则(a+b)(a+b-c)>0,进一步a2+b2+2ab-ac-bc>0,整理得[2(a+b)+1](c+1)<(a+b+1)(a+b+c+1),
不行可得$\frac{c+1}{a+b+c+1}$<$\frac{a+b+1}{2(a+b)+1}$,得到(4)正确.
解答 解:对于(1),原命题“若x=3,则x2-7x+12=0”,则
其逆命题是“若x2-7x+12=0,则x=3”;
否命题是“若x≠3,则x2-7x+12≠0”;
逆否命题是“若x2-7x+12≠0,则x≠3”.
当x=3时,x2-7x+12=0成立,即原命题正确,因此逆否命题也正确;
而x=4时,x2-7x+12=0成立,∴由x≠3,推不出x2-7x+12≠0,即否命题是错误的,因此逆命题也是错误的,
可知四个命题中,正确的命题有2个,故(1)正确;
对于(2),根据柯西不等式,得(a+2b+3c)2=(1×a+1×2b+1×3c)2≤(12+12+12)[a2+(2b)2+(3c)2],
化简得62≤3(a2+4b2+9c2),即36≤3(a2+4b2+9c2),∴a2+4b2+9c2≥12,
当且仅当a:2b:3c=1:1:1时,即a=2,b=1,c=$\frac{2}{3}$时等号成立,由此可得:当且仅当a=2,b=1,c=$\frac{2}{3}$时,a2+4b2+9c2的最小值为12,故(2)正确;
对于(3),根据回归分析的定义可知(3)正确;
对于(4),在△ABC中,∵a+b>c,∴a+b-c>0,则(a+b)(a+b-c)>0,得a2+b2+2ab-ac-bc>0,
∴[2(a+b)+1](c+1)<(a+b+1)(a+b+c+1),得$\frac{c+1}{a+b+c+1}$<$\frac{a+b+1}{2(a+b)+1}$,故(4)正确.
∴真命题的是:(1)(2)(3)(4).
故答案为:(1)(2)(3)(4).
点评 本题考查了命题的真假判断与应用,考查了不等式的应用,是中档题.


科目:高中数学 来源: 题型:填空题
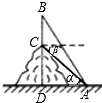 如图,山顶上有一座铁塔,在地面上一点A处测得塔顶B处的仰角α=60°,在山顶C处测得A点的俯角β=45°,已知塔高BC为50m,则山高CD等于25$({\sqrt{3}+1})$m.
如图,山顶上有一座铁塔,在地面上一点A处测得塔顶B处的仰角α=60°,在山顶C处测得A点的俯角β=45°,已知塔高BC为50m,则山高CD等于25$({\sqrt{3}+1})$m.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 25π | B. | 26π | C. | 27π | D. | 28π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{1}{2}$ | C. | 4 | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com