
如图所示的多面体中,  是菱形,
是菱形,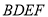 是矩形,
是矩形,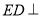 面
面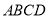 ,
,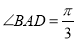 .
.
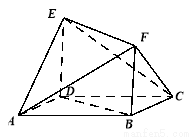
(1)求证:平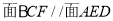 ;
;
(2)若 ,求四棱锥
,求四棱锥 的体积.
的体积.
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源:2015届广东省清远市高二下学期期末文科数学试卷(解析版) 题型:选择题
用反证法证明命题“若 a,b∈N,ab能被3整除,那么a,b中至少有一个能被3整除”时,假设应为( )
A.a,b都能被3整除 B.a不能被3整除
C.a,b不都能被3整除 D.a,b都不能被3整除
查看答案和解析>>
科目:高中数学 来源:2015届广东省梅州市高二下学期期中文科数学试卷(解析版) 题型:填空题
设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为=0.85x-85.71,给定下列结论:
①y与x具有正的线性相关关系;
②回归直线过样本点的中心( ,
, );
);
③若该大学某女生身高增加1cm,则其体重约增加0.85kg;
④若该大学某女生身高为170cm,则可断定其体重必为58.79kg.
其中正确的结论是 .
查看答案和解析>>
科目:高中数学 来源:2015届广东省梅州市高二下学期期中文科数学试卷(解析版) 题型:选择题
已知椭圆与双曲线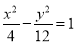 的焦点相同,且椭圆上任意一点到两焦点的距离之和为
的焦点相同,且椭圆上任意一点到两焦点的距离之和为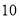 ,那么椭圆的离心率等于( )
,那么椭圆的离心率等于( )
A.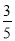 B.
B.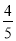 C.
C. D.
D.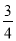
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com