
【题目】设椭圆![]() :
:![]() (
(![]() )的右焦点为
)的右焦点为![]() ,短轴的一个端点
,短轴的一个端点![]() 到
到![]() 的距离等于焦距.
的距离等于焦距.
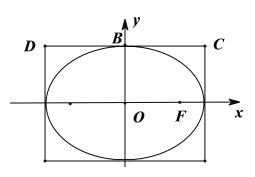
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设![]() 、
、![]() 是四条直线
是四条直线![]() ,
,![]() 所围成的矩形在第一、第二象限的两个顶点,
所围成的矩形在第一、第二象限的两个顶点,![]() 是椭圆
是椭圆![]() 上任意一点,若
上任意一点,若![]() ,求证:
,求证:![]() 为定值;
为定值;
(3)过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() 、
、![]() ,且满足△
,且满足△![]() 与△
与△![]() 的面积的比值为
的面积的比值为![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(1)![]() (2)证明见解析(3)
(2)证明见解析(3)![]()
【解析】
(1)根据椭圆焦点坐标求得![]() ,根据短轴端点到焦点的距离求得
,根据短轴端点到焦点的距离求得![]() ,由此求得
,由此求得![]() ,进而求得椭圆的标准方程.
,进而求得椭圆的标准方程.
(2)求得![]() 的坐标,设出
的坐标,设出![]() 点坐标
点坐标![]() ,结合向量的坐标运算,由
,结合向量的坐标运算,由![]() 求得
求得 ,也即求得
,也即求得![]() 点坐标,将其代入椭圆,化简后证得
点坐标,将其代入椭圆,化简后证得![]() 为定值.
为定值.
(3)将三角形![]() 和三角形
和三角形![]() 的面积的比值,转化为边长的比值,即
的面积的比值,转化为边长的比值,即![]() .当直线
.当直线![]() 斜率不存在时,根据椭圆的对称性可知
斜率不存在时,根据椭圆的对称性可知![]() ,不符合题意.当直线
,不符合题意.当直线![]() 的斜率不存在时,设出直线
的斜率不存在时,设出直线![]() 的方程
的方程![]() .代入椭圆方程,化简后写出韦达定理.由
.代入椭圆方程,化简后写出韦达定理.由![]() ,求得
,求得![]() ,代入韦达定理,由此解方程求得
,代入韦达定理,由此解方程求得![]() 的值,进而求得直线
的值,进而求得直线![]() 的方程.
的方程.
(1)由已知,![]() ,
,
又![]() ,故
,故![]() ,
,
所以,![]() ,所以,椭圆
,所以,椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)![]() ,
,![]() ,
,
设![]() ,则
,则![]() ,
,
由已知![]() ,即
,即![]() ,
,
所以 ,所以
,所以![]() ,化简得
,化简得![]() 为定值.
为定值.
(3)![]() 等价于
等价于![]() ,
,
当直线![]() 的斜率不存在时,
的斜率不存在时,![]() ,不合题意.
,不合题意.
故直线![]() 的斜率存在,设
的斜率存在,设![]() :
:![]() ,
,
由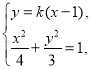 消去
消去![]() ,得
,得![]() ,
,
设![]() ,
,![]() ,则
,则![]() ①,
①,![]() ②,
②,
由![]() ,得
,得![]() ,
,![]() ,将其代入①②,得
,将其代入①②,得![]() ③,
③,![]() ④.将③代入④,化简得
④.将③代入④,化简得![]() ,解得
,解得![]() .
.
所以,直线![]() 的方程为
的方程为![]() .
.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:
【题目】如图一块长方形区域![]() ,
,![]() ,
,![]() ,在边
,在边![]() 的中点
的中点![]() 处有一个可转动的探照灯,其照射角
处有一个可转动的探照灯,其照射角![]() 始终为
始终为![]() ,设
,设![]() ,探照灯照射在长方形
,探照灯照射在长方形![]() 内部区域的面积为
内部区域的面积为![]() .
.
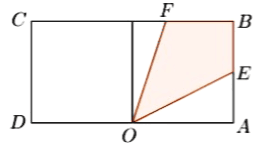
(1)当![]() 时,求
时,求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)当![]() 时,求
时,求![]() 的最大值;
的最大值;
(3)若探照灯每9分钟旋转“一个来回”(![]() 自
自![]() 转到
转到![]() ,再回到
,再回到![]() ,称“一个来回”,忽略
,称“一个来回”,忽略![]() 在
在![]() 及
及![]() 处所用的时间),且转动的角速度大小一定,设
处所用的时间),且转动的角速度大小一定,设![]() 边上有一点
边上有一点![]() ,且
,且![]() ,求点
,求点![]() 在“一个来回”中被照到的时间.
在“一个来回”中被照到的时间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】足球是世界普及率最高的运动,我国大力发展校园足球.为了解本地区足球特色学校的发展状况,社会调查小组得到如下统计数据:
年份x | 2014 | 2015 | 2016 | 2017 | 2018 |
足球特色学校y(百个) | 0.30 | 0.60 | 1.00 | 1.40 | 1.70 |
(1)根据上表数据,计算y与x的相关系数r,并说明y与x的线性相关性强弱.
(已知:![]() ,则认为y与x线性相关性很强;
,则认为y与x线性相关性很强;![]() ,则认为y与x线性相关性一般;
,则认为y与x线性相关性一般;![]() ,则认为y与x线性相关性较):
,则认为y与x线性相关性较):
(2)求y关于x的线性回归方程,并预测A地区2020年足球特色学校的个数(精确到个).
参考公式和数据: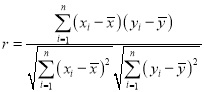 ,
,
![]()
![]()
![]() ,
,
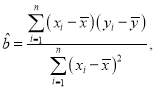
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班学生中喜爱看综艺节目的有18人,体育节目的有27人,时政节目的有9人,现采取分层抽样的方法从这些学生中抽取6名学生.
(Ⅰ)求应从喜爱看综艺节目,体育节目,时政节目的学生中抽取的学生人数;
(Ⅱ)若从抽取的6名学生中随机抽取2人分作一组,
(1)列出所有可能的结果;
(2)求抽取的2人中有1人喜爱综艺节目1人喜爱体育节目的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业参加![]() 项目生产的工人为
项目生产的工人为![]() 人,平均每人每年创造利润
人,平均每人每年创造利润![]() 万元.根据现实的需要,从
万元.根据现实的需要,从![]() 项目中调出
项目中调出![]() 人参与
人参与![]() 项目的售后服务工作,每人每年可以创造利润
项目的售后服务工作,每人每年可以创造利润![]() 万元(
万元(![]() ),
),![]() 项目余下的工人每人每年创造利图需要提高
项目余下的工人每人每年创造利图需要提高![]()
(1)若要保证![]() 项目余下的工人创造的年总利润不低于原来
项目余下的工人创造的年总利润不低于原来![]() 名工人创造的年总利润,则最多调出多少人参加
名工人创造的年总利润,则最多调出多少人参加![]() 项目从事售后服务工作?
项目从事售后服务工作?
(2)在(1)的条件下,当从![]() 项目调出的人数不能超过总人数的
项目调出的人数不能超过总人数的![]() 时,才能使得
时,才能使得![]() 项目中留岗工人创造的年总利润始终不低于调出的工人所创造的年总利润,求实数
项目中留岗工人创造的年总利润始终不低于调出的工人所创造的年总利润,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() ,如果满足:对任意
,如果满足:对任意![]() ,存在常数
,存在常数![]() ,都有
,都有![]() 成立,则称
成立,则称![]() 是
是![]() 上的有界函数,其中
上的有界函数,其中![]() 称为函数
称为函数![]() 的上界.
的上界.
(1)设![]() ,判断
,判断![]() 在
在![]() 上是否为有界函数,若是,请说明理由,并写出
上是否为有界函数,若是,请说明理由,并写出![]() 的所有上界
的所有上界![]() 的集合;若不是,也请说明理由;
的集合;若不是,也请说明理由;
(2)若函数![]() 在
在![]() 上是以
上是以![]() 为上界的有界函数,求实数
为上界的有界函数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产的某批产品的销售量![]() 万件(生产量与销售量相等)与促销费用
万件(生产量与销售量相等)与促销费用![]() 万元满足
万元满足![]() (其中
(其中![]() ,
,![]() 为正常数).已知生产该产品还需投入成本
为正常数).已知生产该产品还需投入成本![]() 万元(不含促销费用),产品的销售价格定为
万元(不含促销费用),产品的销售价格定为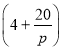 元
元![]() 件.
件.
(1)将该产品的利润![]() 万元表示为促销费用
万元表示为促销费用![]() 万元的函数;
万元的函数;
(2)促销费用投入多少万元时,该公司的利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)设椭圆![]() 与双曲线
与双曲线![]() 有相同的焦点
有相同的焦点![]() 、
、![]() ,
,![]() 是椭圆
是椭圆![]() 与双曲线
与双曲线![]() 的公共点,且△
的公共点,且△![]() 的周长为6,求椭圆
的周长为6,求椭圆![]() 的方程;我们把具有公共焦点、公共对称轴的两段圆锥曲线弧合成的封闭曲线称为“盾圆”;
的方程;我们把具有公共焦点、公共对称轴的两段圆锥曲线弧合成的封闭曲线称为“盾圆”;
(2)如图,已知“盾圆![]() ”的方程为
”的方程为![]() ,设“盾圆
,设“盾圆![]() ”上的任意一点
”上的任意一点![]() 到
到![]() 的距离为
的距离为![]() ,
,![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求证:
,求证:![]() 为定值;
为定值;
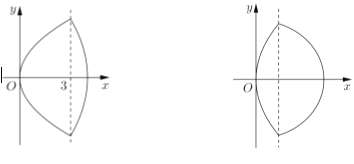
(3)由抛物线弧![]() (
(![]() )与第(1)小题椭圆弧
)与第(1)小题椭圆弧![]()
![]() (
(![]() )所合成的封闭曲线为“盾圆
)所合成的封闭曲线为“盾圆![]() ”,设过点
”,设过点![]() 的直线与“盾圆
的直线与“盾圆![]() ”交于
”交于![]() 、
、![]() 两点,
两点,![]() ,
,![]() ,且
,且![]() (
(![]() ),试用
),试用![]() 表示
表示![]() ,并求
,并求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,四边形![]() 是正方形,四边形
是正方形,四边形![]() 是梯形,
是梯形,![]() ∥
∥![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() .
.
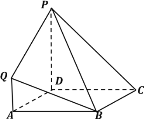
(Ⅰ)求证:![]() ∥平面
∥平面![]() ;
;
(Ⅱ)求二面角![]() 的大小;
的大小;
(Ⅲ)已知点![]() 在棱
在棱![]() 上,且异面直线
上,且异面直线![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com