
如图,已知 是正三棱柱,它的底面边长和侧棱长都是2,D为侧棱
是正三棱柱,它的底面边长和侧棱长都是2,D为侧棱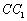 的中点,
的中点,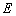 为
为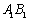 的中点.
的中点.
(1)求证: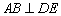 ;
;
(2)求直线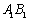 到平面
到平面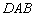 的距离;
的距离;
(3)求二面角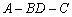 的正切值.
的正切值.
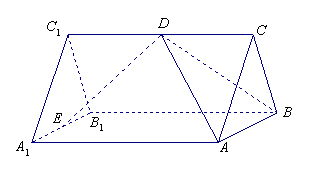
解:(1)证明:连结C1E,则C1E^A1B1,
又∵A1B1^C1C,∴A1B1^平面EDC1,∴A1B1^DE,
而A1B1//AB,∴AB^DE. ……………3分
(2)取AB中点为F,连结EF,DF,则EF^AB,∴AB^DF.
过E作直线EH^DF于H点,则EH^平面DAB,∴EH就是直线A1B1到平面DAB的距离. 在矩形C1EFC中,∵AA1=AB=2,∴EF=2,C1E=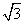 ,DF=2,
,DF=2,
∴在△DEF中,EH=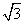 ,……………7分
,……………7分
故直线A1B1到平面DAB的距离为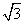 .
.
(3)过A作AM^BC于M点,则AM^平面CDB,
过M作MN^BD于N点,连结AN,则AN^BD,∴∠ANM即为所求二面角的平面角,
在Rt△DCB中,BC=2,DC=1,M为BC中点,∴MN=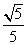 ,
,
在Rt△AMN中,tan∠ANM=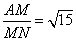 ……………12分
……………12分


科目:高中数学 来源: 题型:
设F1,F2分别为双曲线C: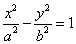 (a>0,b>0)的左、右焦点,A为双曲线的左顶点,以F1F2为直径的圆交双曲线某条渐近线于M、N两点,且满足
(a>0,b>0)的左、右焦点,A为双曲线的左顶点,以F1F2为直径的圆交双曲线某条渐近线于M、N两点,且满足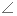 MAN=120o,则该双曲线的离心率为 ( )
MAN=120o,则该双曲线的离心率为 ( )
A. 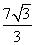 B.
B. 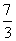 C.
C. 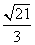 D.
D.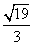
查看答案和解析>>
科目:高中数学 来源: 题型:
设某中学高三的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为y=0.85x﹣85.71,则下列结论中不正确的是( )
A. y与x具有正的线性相关关系
B. 回归直线过样本点的中心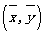
C. 若该中学高三某女生身高增加1cm,则其体重约增加0.85kg
D. 若该中学高三某女生身高为170cm,则可断定其体重必为58.79kg
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com