
|
|
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
| 3a+2 |
| 2 |
| 3a+2 |
| 2 |
| 5 |
| 2 |
| ||
| 2 |


 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:
| x+1 |
| x-1 |
| 1-x2 |
| 1+x2 |
| 1-x |
查看答案和解析>>
科目:高中数学 来源: 题型:
| PE |
| 1 |
| 3 |
| ED |
查看答案和解析>>
科目:高中数学 来源: 题型:
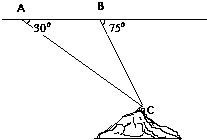 如图,飞机的航线和山顶在同一铅垂面内,若飞机的高度为海拔18km,速度为1000km/h,飞行员先看到山顶的俯角为30°,经过1min后又看到山顶的俯角为75°,则山顶的海拔高度为(精确到0.1)( )
如图,飞机的航线和山顶在同一铅垂面内,若飞机的高度为海拔18km,速度为1000km/h,飞行员先看到山顶的俯角为30°,经过1min后又看到山顶的俯角为75°,则山顶的海拔高度为(精确到0.1)( )| A、11.4 | B、6.6 |
| C、6.5 | D、5.6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com