
已知函数 ,
, .
.
证明:(1)存在唯一 ,使
,使 ;
;
(2)存在唯一 ,使
,使 ,且对(1)中的
,且对(1)中的 .
.
科目:高中数学 来源: 题型:解答题
已知二次函数f(x)=x2+2bx+c(b、c∈R).
(1)若f(x)≤0的解集为{x|-1≤x≤1},求实数b、c的值;
(2)若f(x)满足f(1)=0,且关于x的方程f(x)+x+b=0的两个实数根分别在区间(-3,-2),(0,1)内,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)对任意实数x,y恒有f(x+y)=f(x)+f(y),且当x>0时,f(x)<0,又f(1)=-2.
(1)判断f(x)的奇偶性;
(2)求证:f(x)是R上的减函数;
(3)求f(x)在区间[-3,3]上的值域;
(4)若?x∈R,不等式f(ax2)-2f(x)<f(x)+4恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某小区想利用一矩形空地 建市民健身广场,设计时决定保留空地边上的一水塘(如图中阴影部分),水塘可近似看作一个等腰直角三角形,其中
建市民健身广场,设计时决定保留空地边上的一水塘(如图中阴影部分),水塘可近似看作一个等腰直角三角形,其中 ,
, ,且
,且 中,
中, ,经测量得到
,经测量得到 .为保证安全同时考虑美观,健身广场周围准备加设一个保护栏.设计时经过点
.为保证安全同时考虑美观,健身广场周围准备加设一个保护栏.设计时经过点 作一直线交
作一直线交 于
于 ,从而得到五边形
,从而得到五边形 的市民健身广场,设
的市民健身广场,设 .
.
(1)将五边形 的面积
的面积 表示为
表示为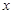 的函数;
的函数;
(2)当 为何值时,市民健身广场的面积最大?并求出最大面积.
为何值时,市民健身广场的面积最大?并求出最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如果函数 的定义域为R,对于定义域内的任意
的定义域为R,对于定义域内的任意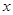 ,存在实数
,存在实数 使得
使得 成立,则称此函数具有“
成立,则称此函数具有“ 性质”。
性质”。
(1)判断函数 是否具有“
是否具有“ 性质”,若具有“
性质”,若具有“ 性质”,求出所有
性质”,求出所有 的值;若不具有“
的值;若不具有“ 性质”,说明理由;
性质”,说明理由;
(2)已知 具有“
具有“ 性质”,且当
性质”,且当 时
时 ,求
,求 在
在 上有最大值;
上有最大值;
(3)设函数 具有“
具有“ 性质”,且当
性质”,且当 时,
时, .若
.若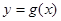 与
与 交点个数为2013,求
交点个数为2013,求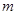 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
某地街道呈现东—西、南—北向的网格状,相邻街距都为1.两街道相交的点称为格点.若以互相垂直的两条街道为轴建立直角坐标系,现有下述格点 ,
, ,
, ,
, ,
, ,
, 为报刊零售点.请确定一个格点(除零售点外)__________为发行站,使6个零售点沿街道到发行站之间路程的和最短.
为报刊零售点.请确定一个格点(除零售点外)__________为发行站,使6个零售点沿街道到发行站之间路程的和最短.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com