
分析 设出P(x,y)(x>0,y<0),由题意列关于x,y的方程组,求解方程组得答案.
解答 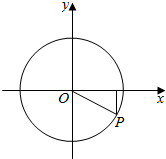 解:如图,
解:如图,
设P(x,y)(x>0,y<0),
∵tanα=-$\frac{3}{4}$,
∴$\frac{y}{x}=-\frac{3}{4}$ ①,
又x2+y2=1 ②,
联立①②解得:$\left\{\begin{array}{l}{x=\frac{4}{5}}\\{y=-\frac{3}{5}}\end{array}\right.$.
∴点P的坐标为($\frac{4}{5},-\frac{3}{5}$).
故答案为:($\frac{4}{5},-\frac{3}{5}$).
点评 本题考查任意角的三角函数的定义,是基础的计算题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2x+y+2=0 | B. | 2x+y+3=0 | C. | 2x-y-1=0 | D. | 2x-y+1=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5π}{3}$ | B. | $\frac{2}{3}$π | C. | $\frac{5}{6}$π | D. | $\frac{11}{6}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
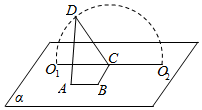 如图,A,B,C,O1,O2∈平面α,AB=BC=$\sqrt{3}$,∠ABC=90°,D为动点,DC=2,且DC丄BC,当点D从O1,顺时针转动到O2的过程中(D与O1、O2不重合),异面直线AD与BC所成角( )
如图,A,B,C,O1,O2∈平面α,AB=BC=$\sqrt{3}$,∠ABC=90°,D为动点,DC=2,且DC丄BC,当点D从O1,顺时针转动到O2的过程中(D与O1、O2不重合),异面直线AD与BC所成角( )| A. | 一直变小 | B. | 一直变大 | ||
| C. | 先变小,后变大 | D. | 先变小,再变大,后变小 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com