Question

6．已知圆O的半径为2，A，B是圆O上任意两点，且∠AOB=120°，PQ是圆O的一条直径，若点C满足$\overrightarrow{OC}=3λ\overrightarrow{OA}+3（{1-λ}）\overrightarrow{OB}（{λ∈R}）$，则$\overrightarrow{CP}•\overrightarrow{CQ}$的最小值为（　　）

• A． 3
• B． 4
• C． 5
• D． 6

Answer 1

分析 可以O为坐标原点，OB所在直线为x轴，建立平面直角坐标系，根据条件可求出A，B点的坐标，可设P（2cosθ，2sinθ），Q（-2cosθ，-2sinθ），这样根据$\overrightarrow{OC}=3λ\overrightarrow{OA}+3（1-λ）\overrightarrow{OB}$即可求出向量$\overrightarrow{OC}$的坐标，从而得到点C的坐标．这样即可求出$\overrightarrow{CP}，\overrightarrow{CQ}$的坐标，进行数量积的坐标运算便可得到$\overrightarrow{CP}•\overrightarrow{CQ}=4（27{λ}^{2}-27λ+8）$，从而根据二次函数最值的计算公式便可求出4（27λ²-27λ+8）的最小值，即求出$\overrightarrow{CP}•\overrightarrow{CQ}$的最小值．

解答 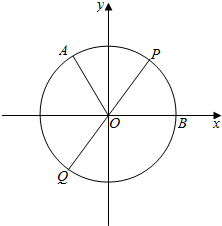解：以O为原点，OB所在直线为x轴，建立如图所示平面直角坐标系，则：
$A（-1，\sqrt{3}），B（2，0）$；
根据题意，设P（2cosθ，2sinθ），Q（-2cosθ，-2sinθ）；
$\overrightarrow{OC}=3λ（-1，\sqrt{3}）+3（1-λ）（2，0）$=$（6-9λ，3\sqrt{3}λ）$；
∴$C（6-9λ，3\sqrt{3}λ）$；
∴$\overrightarrow{CP}=（2cosθ+9λ-6，2sinθ-3\sqrt{3}λ）$，$\overrightarrow{CQ}=（-2cosθ+9λ-6，-2sinθ-3\sqrt{3}λ）$；
∴$\overrightarrow{CP}•\overrightarrow{CQ}=（9λ-6）^{2}-4co{s}^{2}θ$+27λ²-4sin²θ
=4（27λ²-27λ+8）$≥4×\frac{4×27×8-2{7}^{2}}{4×27}=5$．
∴$\overrightarrow{CP}•\overrightarrow{CQ}$的最小值为5．
故选：C．

点评 考查通过建立平面直角坐标系，利用向量的坐标解决向量问题的方法，能求图形上点的坐标，根据点的坐标求向量的坐标，向量坐标的加法和数乘运算，以及数量积的坐标运算，二次函数最值的计算公式．