
若关于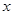 的方程
的方程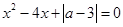 有实根
有实根
(Ⅰ)求实数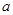 的取值集合
的取值集合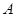
(Ⅱ)若对于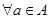 ,不等式
,不等式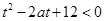 恒成立,求
恒成立,求 的取值范围
的取值范围
(Ⅰ)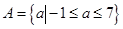 ;(Ⅱ)
;(Ⅱ) 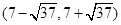 。
。
解析试题分析:(Ⅰ)∵关于x的方程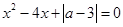 有实根,
有实根,
∴△=16-4|a-3|≥0,即|a-3|≤4,
∴-4≤a-3≤4,∴-1≤a≤7,故实数a的取值集合A={a|-1≤a≤7 };
(Ⅱ)∵对于?a∈A,不等式t2-2at+12<0恒成立,令f(a)=-2at+t2+12,则f(a)<0 恒成立.
故 f(-1)<0 且f(7)<0,即 2t+t2+12<0 ①,且-14t+t2+12<0 ②.
解①得 t∈∅,解②得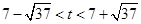 .
.
综上可得,t的取值范围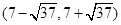 . 10分
. 10分
考点:一元二次不等式解法,不等式恒成立问题。
点评:中档题,对于二次函数的根的问题,变更主元,构造函数f(a)=t2-2a|t|+12,转化为函数的最小值是解题的关键和难点。


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com