
分析 根据D是△ABC的边AB上一点,设$\overrightarrow{DB}=k\overrightarrow{AB}$,(0<k<1),然后把$\overrightarrow{CD}$用$\overrightarrow{CA},\overrightarrow{CB}$表示即可.
解答 解:∵D是△ABC的边AB上一点,设$\overrightarrow{DB}=k\overrightarrow{AB}$,(0<k<1)则$\overrightarrow{AD}=(1-k)\overrightarrow{AB}$,
又$\overrightarrow{CD}=\overrightarrow{CA}+\overrightarrow{AD}$,
$\overrightarrow{CD}=\overrightarrow{CB}+\overrightarrow{BD}$,
∴2$\overrightarrow{CD}$=$\overrightarrow{CA}+\overrightarrow{CB}+(1-2k)(\overrightarrow{CB}-\overrightarrow{CA})$,
∴$\overrightarrow{CD}=k\overrightarrow{CA}+(1-k)\overrightarrow{CB}$,
∵$\overrightarrow{CD}$=λ$\overrightarrow{CA}$+λ2$\overrightarrow{CB}$,
∴$\left\{\begin{array}{l}{λ=k}\\{1-k={λ}^{2}}\end{array}\right.$,
解得:$λ=\frac{\sqrt{5}-1}{2}$或$-\frac{\sqrt{5}+1}{2}$(舍),
故答案为:$\frac{\sqrt{5}-1}{2}$.
点评 本题主要考查向量的共线和平面向量基本定理,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | 2 | D. | -3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
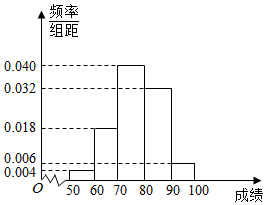 到2016年,北京市高考英语总分将由150分降低到100分,语文分值将相应增加.某校高三学生率先尝试100分制英语考试,从中随机抽出50人的英语成绩作为样本并进行统计,将测试结果按如下方式分成五组:第一组[50,60],第二组[60,70],…第五组[90,100],如图是按上述分组方法得到的频率分布直方图.
到2016年,北京市高考英语总分将由150分降低到100分,语文分值将相应增加.某校高三学生率先尝试100分制英语考试,从中随机抽出50人的英语成绩作为样本并进行统计,将测试结果按如下方式分成五组:第一组[50,60],第二组[60,70],…第五组[90,100],如图是按上述分组方法得到的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{11}{15}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com