
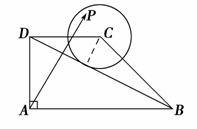
如图,在直角梯形ABCD中,AD⊥AB,AB∥DC,AD=DC=1,AB=2,动点P在以点C为圆心,且与直线BD相切的圆上或圆内移动,设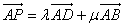 (λ,μ∈R),则λ+μ的取值范围是( )
(λ,μ∈R),则λ+μ的取值范围是( )
A.(1,2) B.(0,3)
C.[1,2] D.[1,2)
科目:高中数学 来源: 题型:
若对任意x∈A,y∈B,(A⊆R,B⊆R)有唯一确定的f(x ,y)与之对应,则称f(x,y)为关于x,y的二元函数.满足下列性质的二元函数
,y)与之对应,则称f(x,y)为关于x,y的二元函数.满足下列性质的二元函数 f(x,y)称为关于实数x,y的广义“距离”:
f(x,y)称为关于实数x,y的广义“距离”:
(1)非负性:f(x,y)≥0,当且仅当x=y时取等号;
(2)对称性:f(x,y)=f(y,x);
(3)三角形不等式:f(x,y)≤f(x,z)+f(z,y)对任意的实数z均成立.
今给出三个二元函数:①f(x,y)=|x-y|;②f(x,y)=(x-y)2;③f(x,y)=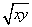 .
.
其中能够成为关于x,y的广义“距离”的二元函数的序号是( )
A.① B.①② C.②③ D.①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
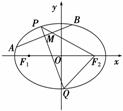
已知椭圆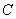 :
: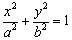 (
(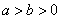 )的焦距为
)的焦距为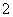 ,且过点(
,且过点(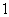 ,
,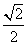 ),右焦点为
),右焦点为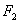 .设
.设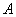 ,
,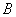 是
是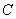 上的两个动点,线段
上的两个动点,线段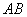 的中点
的中点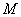 的横坐标为
的横坐标为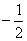 ,
, 线段
线段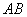 的中垂线交椭圆
的中垂线交椭圆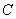 于
于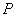 ,
,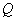 两点.
两点.
 (Ⅰ)求椭圆
(Ⅰ)求椭圆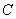 的方程;
的方程;
(Ⅱ)求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
一辆汽车在高速公路上行驶,由于遇到紧急情况而刹车,以速度v(t)=7-3t+ 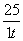 (t的单位:s,v
(t的单位:s,v 的单位:m/s)行驶至停止.在此期间汽车继续行驶的距离(单位:m)是( )
的单位:m/s)行驶至停止.在此期间汽车继续行驶的距离(单位:m)是( )
A.1+25ln 5 B.8+25ln 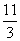 C.4+25ln 5
C.4+25ln 5  D.4+50ln 2
D.4+50ln 2
查看答案和解析>>
科目:高中数学 来源: 题型:
某实验室一天的温度(单位:℃)随时间t(单位:h)的变化近似满足函数关系:
f(t)=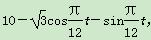 ,t∈[0,24).
,t∈[0,24).
(1)求实验室这一天的最大温差.
(2)若要求实验室温度不高于11℃,则在哪段时间实验室需要降温?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com