
设a=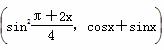 ,b=(4sinx,cosx-sinx),f(x)=a·b.
,b=(4sinx,cosx-sinx),f(x)=a·b.
(1) 求函数f(x)的解析式;
(2) 已知常数ω>0,若y=f(ωx)在区间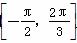 上是增函数,求ω的取值范围;
上是增函数,求ω的取值范围;
(3) 设集合A= ,B={x||f(x)-m|<2},若AB,求实数m的取值范围.
,B={x||f(x)-m|<2},若AB,求实数m的取值范围.
解:(1) f(x)=sin2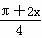 ·4sinx+(cosx+sinx)·(cosx-sinx)
·4sinx+(cosx+sinx)·(cosx-sinx)
=4sinx·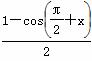 +cos2x
+cos2x
=2sinx(1+sinx)+1-2sin2x=2sinx+1,
所以所求解析式为f(x)=2sinx+1.
(2) ∵f(ωx)=2sinωx+1,ω>0,
由2kπ-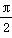 ≤ωx≤2kπ+
≤ωx≤2kπ+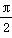 ,
,
得f(ωx)的增区间是 ,k∈Z.
,k∈Z.
∵f(ωx)在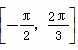 上是增函数,
上是增函数,
∴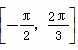
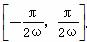 .
.
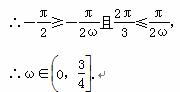
(3) 由|f(x)-m|<2,得-2<f(x)-m<2,
即f(x)-2<m<f(x)+2.
∵AB,∴当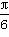 ≤x≤
≤x≤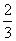 π时,
π时,
不等式f(x)-2<m<f(x)+2恒成立.
∴f(x)max-2<m<f(x)min+2,
∵f(x)max=f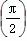 =3,f(x)min=f
=3,f(x)min=f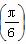 =2,
=2,
∴m∈(1,4).


科目:高中数学 来源: 题型:
已知一扇形的中心角是α,所在圆的半径是R.
(1) 若α=60°,R=10cm,求扇形的弧长及该弧所在的弓形面积;
(2) 若扇形的周长是一定值C(C>0),当α为多少弧度时,该扇形有最大面积?
查看答案和解析>>
科目:高中数学 来源: 题型:
已知椭圆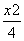 +y2=1的左顶点为A,过A作两条互相垂直的弦AM、AN交椭圆于M、N两点.
+y2=1的左顶点为A,过A作两条互相垂直的弦AM、AN交椭圆于M、N两点.
(1) 当直线AM的斜率为1时,求点M的坐标;
(2) 当直线AM的斜率变化时,直线MN是否过x轴上的一定点?若过定点,请给出证明,并求出该定点;若不过定点,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com