
分析 (1)由条件利用正弦函数的周期性、值域,得出结论.
(2)由条件利用正弦函数的单调性求得函数的单调区间.
解答 解:(1)根据函数$f(x)=\sqrt{2}cos({x+\frac{π}{4}})$,x∈R,可得周期T=2π,且 $y∈[{-\sqrt{2},\sqrt{2}}]$.
(2)令2kπ-$\frac{π}{2}$≤x+$\frac{π}{4}$≤2kπ+$\frac{π}{2}$,求得2kπ-$\frac{3π}{4}$≤x≤2kπ+$\frac{π}{4}$,可得函数的单调增区间为:[2kπ-$\frac{3π}{4}$,2kπ+$\frac{π}{4}$],k∈Z.
令2kπ+$\frac{π}{2}$≤x+$\frac{π}{4}$≤2kπ+$\frac{3π}{2}$,求得2kπ+$\frac{π}{4}$≤x≤2kπ+$\frac{5π}{4}$,可得函数的单调减区间为:[2kπ+$\frac{π}{4}$,2kπ+$\frac{5π}{4}$],k∈Z.
点评 本题主要考查正弦函数的周期性、值域,正弦函数的单调性,属于基础题.


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:选择题
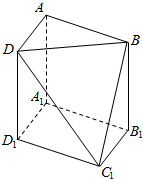 在如图所示的几何体ABD-A1B1C1D1中,底面A1B1C1D1是矩形,AA1⊥平面A1B1C1D1,且AA1平行且等于BB1平行且等于DD1,若∠DC1D1=-$\frac{π}{4}$,∠BC1B1=$\frac{π}{3}$,BC1=2,则该几何体的体积是( )
在如图所示的几何体ABD-A1B1C1D1中,底面A1B1C1D1是矩形,AA1⊥平面A1B1C1D1,且AA1平行且等于BB1平行且等于DD1,若∠DC1D1=-$\frac{π}{4}$,∠BC1B1=$\frac{π}{3}$,BC1=2,则该几何体的体积是( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{8}{3}$ | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1$ | B. | $\frac{{x}^{2}}{36}+\frac{{y}^{2}}{27}=1$ | C. | $\frac{{x}^{2}}{36}+\frac{{y}^{2}}{9}=1$ | D. | $\frac{{y}^{2}}{36}+\frac{{x}^{2}}{27}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,棱柱ABCD-A1B1C1D1的底面是菱形,∠DAB=60°,AA1⊥面ABCD,且AD=AA1=1,F为棱AA1的中点,M为线段BD1的中点.
如图,棱柱ABCD-A1B1C1D1的底面是菱形,∠DAB=60°,AA1⊥面ABCD,且AD=AA1=1,F为棱AA1的中点,M为线段BD1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x+y-2=0 | B. | x+y-3=0 | C. | 2x-y-3=0 | D. | 2x+y-3=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com