
【题目】已知点![]() ,动点
,动点![]() 到直线
到直线![]() 的距离与动点
的距离与动点![]() 到点
到点![]() 的距离之比为
的距离之比为![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 作任一直线交曲线
作任一直线交曲线![]() 于
于![]() ,
,![]() 两点,过点
两点,过点![]() 作
作![]() 的垂线交直线
的垂线交直线![]() 于点
于点![]() ,求证:
,求证:![]() 平分线段
平分线段![]() .
.
 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:
【题目】已知某运动员每次投篮命中的概率低于![]() ,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了如下20组随机数:
,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了如下20组随机数:
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
据此估计,该运动员三次投篮恰有两次命中的概率为( )
A.0.35B.0.25C.0.20D.0.15
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为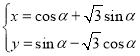 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,取相同长度单位建立极坐标系,直线
轴的正半轴为极轴,取相同长度单位建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 和直线
和直线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)直线![]() 与
与![]() 轴交点为
轴交点为![]() ,经过点
,经过点![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() ,
,![]() 两点,证明:
两点,证明:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】诚信是立身之本,道德之基,某校学生会创设了“诚信水站”,既便于学生用水,又推进诚信教育,并用“![]() ”表示每周“水站诚信度”,为了便于数据分析,以四周为一周期,下表为该水站连续十二周(共三个周期)的诚信数据统计:
”表示每周“水站诚信度”,为了便于数据分析,以四周为一周期,下表为该水站连续十二周(共三个周期)的诚信数据统计:
第一周 | 第二周 | 第三周 | 第四周 | |
第一个周期 |
|
|
|
|
第二个周期 |
|
|
|
|
第三个周期 |
|
|
|
|
(1)计算表中十二周“水站诚信度”的平均数![]() ;
;
(2)分别从表中每个周期的4个数据中随机抽取1个数据,设随机变量![]() 表示取出的3个数中“水站诚信度”超过
表示取出的3个数中“水站诚信度”超过![]() 的数据的个数,求随机变量
的数据的个数,求随机变量![]() 的分布列和期望;
的分布列和期望;
(3)已知学生会分别在第一个周期的第四周末和第二个周期的第四周末各举行了一次“以诚为本”的主题教育活动,根据已有数据,说明两次主题教育活动的宣传效果,并根据已有数据陈述理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面四边形![]() 中,
中,![]() 、
、![]() 分
分![]() 、
、![]() 所成的比为
所成的比为![]() ,即
,即![]() ,则有:
,则有:![]() .
.

(1)拓展到空间,写出空间四边形![]() 类似的命题,并加以证明;
类似的命题,并加以证明;
(2)在长方体![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,利用上述(1)的结论求线段
的中点,利用上述(1)的结论求线段![]() 的长度;
的长度;
(3)在所有棱长均为![]() 平行六面体
平行六面体![]() 中,
中,![]() (
(![]() 为锐角定值),
为锐角定值),![]() 、
、![]() 分
分![]() 、
、![]() 所成的比为
所成的比为![]() ,求
,求![]() 的长度.(用
的长度.(用![]() ,
,![]() ,
,![]() 表示)
表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业购买某种仪器,在仪器使用期间可能出现故障,需要请销售仪器的企业派工程师进行维修,因为考虑到人力、成本等多方面的原因,销售仪器的企业提供以下购买仪器维修服务的条件:在购买仪器时,可以直接购买仪器维修服务,维修一次1000元;在仪器使用期间,如果维修服务次数不够再次购买,则需要每次1500元..现需决策在购买仪器的同时购买几次仪器维修服务,为此搜集并整理了500台这种机器在使用期内需要维修的次数,得到如下表格:
维修次数 | 5 | 6 | 7 | 8 | 9 |
频数(台) | 50 | 100 | 150 | 100 | 100 |
记![]() 表示一台仪器使用期内维修的次数,
表示一台仪器使用期内维修的次数,![]() 表示一台仪器使用期内维修所需要的费用,
表示一台仪器使用期内维修所需要的费用,![]() 表示购买仪器的同时购买的维修服务的次数.
表示购买仪器的同时购买的维修服务的次数.
(1)若![]() ,求
,求![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)以这500台仪器使用期内维修次数的频率代替一台仪器维修次数发生的概率,求![]() 的概率.
的概率.
(3)假设购买这500台仪器的同时每台都购买7次维修服务,或每台都购买8次维修服务,请分别计算这500台仪器在购买维修服务所需要费用的平均数,以此为决策依据,判断购买7次还是8次维修服务?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在下列向量组中,可以把向量![]() =(3,2)表示出来的是( )
=(3,2)表示出来的是( )
A. ![]() =(0,0),
=(0,0),![]() =(1,2)B.
=(1,2)B. ![]() =(-1,2),
=(-1,2),![]() =(5,-2)
=(5,-2)
C. ![]() =(3,5),
=(3,5),![]() =(6,10)D.
=(6,10)D. ![]() =(2,-3),
=(2,-3),![]() =(-2,3)
=(-2,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】长时间用手机上网严重影响着学生的健康,某校为了解A,B两班学生手机上网的时长,分别从这两个班中随机抽取6名同学进行调查,将他们平均每周手机上网时长作为样本数据,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).如果学生平均每周手机上网的时长大于21小时,则称为“过度用网”
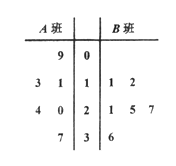
(1)请根据样本数据,分别估计A,B两班的学生平均每周上网时长的平均值;
(2)从A班的样本数据中有放回地抽取2个数据,求恰有1个数据为“过度用网”的概率;
(3)从A班、B班的样本中各随机抽取2名学生的数据,记“过度用网”的学生人数为![]() ,写出
,写出![]() 的分布列和数学期望E
的分布列和数学期望E![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com