Question

20．已知点M（1，2），N（4，3），动点P满足$\overrightarrow{OP}$=λ$\overrightarrow{OM}$+μ$\overrightarrow{ON}$，其中O为坐标原点，且λμ≥0，|λ+μ|≤1，则点P所在平面区域的面积为5．

Answer 1

分析 当λ，μ均大于0时，P点所在区域为△OMN内部，当λ，μ均小于0时，P点所在区域为△OMN关于原点对称的三角形．

解答 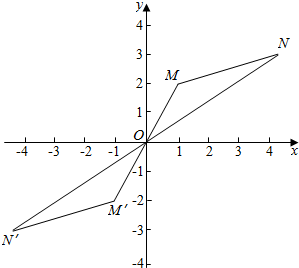解：当λ＞0，μ＞0，0≤λ+μ≤1时，点P所在区域为△OMN内部（含边界），
当λ＜0，μ＜0，-1≤λ+μ≤0时，点P所在区域为△OMN内部（含边界）关于原点得对称区域．
|$\overrightarrow{OM}$|=$\sqrt{5}$，|$\overrightarrow{ON}$|=5，$\overrightarrow{OM}•\overrightarrow{ON}$=10，
∴cos＜$\overrightarrow{OM}$，$\overrightarrow{ON}$＞=$\frac{10}{5\sqrt{5}}$=$\frac{2\sqrt{5}}{5}$，
∴sin＜$\overrightarrow{OM}$，$\overrightarrow{ON}$＞=$\frac{\sqrt{5}}{5}$．
∴S_△OMN=$\frac{1}{2}×$5×$\sqrt{5}$×$\frac{\sqrt{5}}{5}$=$\frac{5}{2}$．
∴点P所在的区域面积S=2S_△OMN=5．
故答案为：5．

点评 本题考查了平面向量的基本定理及其意义，属于基础题．