
【题目】已知抛物线![]() ,直线
,直线![]() 交此抛物线于不同的两个点
交此抛物线于不同的两个点![]() 、
、![]() .
.
(![]() )当直线
)当直线![]() 过点
过点![]() 时,证明
时,证明![]() ,
,![]() 为定值.
为定值.
(![]() )当
)当![]() 时,直线
时,直线![]() 是否过定点?若过定点,求出定点坐标;反之,请说明理由.
是否过定点?若过定点,求出定点坐标;反之,请说明理由.
(![]() )记
)记![]() ,如果直线
,如果直线![]() 过点
过点![]() ,设线段
,设线段![]() 的中点为
的中点为![]() ,线段
,线段![]() 的中点为
的中点为![]() .问是否存在一条直线和一个定点,使得点
.问是否存在一条直线和一个定点,使得点![]() 到它们的距离相等?若存在,求出这条直线和这个定点;若不存在,请说明理由.
到它们的距离相等?若存在,求出这条直线和这个定点;若不存在,请说明理由.
【答案】(1)见解析;(2)![]() ;(3)直线
;(3)直线![]() ,点
,点![]()
【解析】试题分析:(1)易判断直线![]() 有斜率且不为0,设
有斜率且不为0,设![]() ,代入抛物线方程消掉
,代入抛物线方程消掉![]() 得
得![]() 的二次方程,由韦达定理即可证明;
的二次方程,由韦达定理即可证明;
(2)分情况讨论:①当直线![]() 的斜率存在时,设
的斜率存在时,设![]() ,其中
,其中![]() ,代入抛物线方程消掉
,代入抛物线方程消掉![]() 得
得![]() 的二次方程,由韦达定理及
的二次方程,由韦达定理及![]() 得
得![]() 的关系式,假设直线
的关系式,假设直线![]() 过定点
过定点![]() ,则
,则![]() ,用
,用![]() 消掉
消掉![]() 即可得到定点坐标;
即可得到定点坐标;
②当直线![]() 的斜率不存在,设
的斜率不存在,设![]() ,代入抛物线方程易求
,代入抛物线方程易求![]() ,由已知可求得
,由已知可求得![]() 可判断此时直线也过该定点;
可判断此时直线也过该定点;
(3)易判断直线![]() 存在斜率且不为0,由(1)及中点坐标公式可得
存在斜率且不为0,由(1)及中点坐标公式可得![]() ,代入直线
,代入直线![]() 方程得
方程得![]() ,设
,设![]() ,由中点坐标公式可得点
,由中点坐标公式可得点![]() 轨迹的参数方程,消掉参数
轨迹的参数方程,消掉参数![]() 后即得其普通方程,由方程及抛物线定义可得准线、焦点即为所求;
后即得其普通方程,由方程及抛物线定义可得准线、焦点即为所求;
试题解析:(![]() )证明:
)证明:![]() 过点
过点![]() 与抛物线有两个交点,可知其斜率一定存在,
与抛物线有两个交点,可知其斜率一定存在,
设![]() ,其中
,其中![]() (若
(若![]() 时不合题意),
时不合题意),
由![]() 得
得![]() ,
,
∴![]() .
.
(![]() )①当直线
)①当直线![]() 的斜率存在时,设
的斜率存在时,设![]() ,其中
,其中![]() (若
(若![]() 时不合题意).
时不合题意).
由![]() 得
得![]() ,
,
∴![]() ,从而
,从而![]() .
.
假设直线![]() 过定点
过定点![]() ,则
,则![]() ,
,
从而![]() ,得
,得![]() ,即
,即 ,即或定点
,即或定点![]() .
.
②当直线![]() 的斜率不存在,设
的斜率不存在,设![]() ,代入
,代入![]() 得
得![]() ,
,![]() ,
,
∴![]() ,
,
解得![]() ,即
,即![]() ,也过
,也过![]() .
.
综上所述,当![]() 时,直线
时,直线![]() 过定点
过定点![]() .
.
(![]() )依题意直线
)依题意直线![]() 的斜率存在且不为零.
的斜率存在且不为零.
由(![]() )得,点
)得,点![]() 的纵坐标为
的纵坐标为![]() ,
,
代入![]() 得
得![]() ,即
,即![]() .
.
设![]() ,则
,则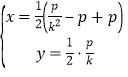 ,消
,消![]() 得
得![]() ,
,
由抛物线的定义知,存在直线![]() ,点
,点![]() ,点
,点![]() 到它们的距离相等.
到它们的距离相等.


科目:高中数学 来源: 题型:
【题目】二战中盟军为了知道德国“虎式”重型坦克的数量,采用了两种方法,一种是传统的情报窃取,一种是用统计学的方法进行估计,统计学的方法最后被证实比传统的情报收集更精确,德国人在生产坦克时把坦克从1开始进行了连续编号,在战争期间盟军把缴获的“虎式”坦克的编号进行记录,并计算出这些编号的平均值为675.5,假设缴获的坦克代表了所有坦克的一个随机样本,则利用你所学过的统计知识估计德国共制造“虎式”坦克大约有( )
A.1050辆
B.1350辆
C.1650辆
D.1950辆
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某某大学艺术专业400名学生参加某次测评,根据男女学生人数比例,使用分层抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组: ![]() ,并整理得到如下频率分布直方图:
,并整理得到如下频率分布直方图:

(Ⅰ)从总体的400名学生中随机抽取一人,估计其分数小于70的概率;
(Ⅱ)已知样本中分数小于40的学生有5人,试估计总体中分数在区间[40,50)内的人数;
(Ⅲ)已知样本中有一半男生的分数不小于70,且样本中分数不小于70的男女生人数相等.试估计总体中男生和女生人数的比例.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直三棱柱![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() 的中点,
的中点,![]() ,
,![]() 为棱
为棱![]() 上的点.
上的点.
(1)证明:![]() ;
;
(2)是否存在一点![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() ?若存在,说明点
?若存在,说明点![]() 的位置,若不存在,说明理由.
的位置,若不存在,说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若
,若![]() ,则称
,则称![]() 为
为![]() 的“不动点”;若
的“不动点”;若![]() ,则称
,则称![]() 为
为![]() 的“稳定点”.函数
的“稳定点”.函数![]() 的“不动点”和“稳定点”的集合分别记为
的“不动点”和“稳定点”的集合分别记为![]() 和
和![]() ,即
,即![]() ,
,![]() .
.
(![]() )设函数
)设函数![]() ,求集合
,求集合![]() 和
和![]() .
.
(![]() )求证:
)求证:![]() .
.
(![]() )设函数
)设函数![]() ,且
,且![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以O为极点,x轴的正半轴为极轴建立极坐标系,曲线C:ρ2﹣4ρcosθ+1=0,直线l: ![]() (t为参数,0≤α<π).
(t为参数,0≤α<π).
(1)求曲线C的参数方程;
(2)若直线l与曲线C相切,求直线l的倾斜角及切点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,平面五边形ABCDE中,AB∥CD,∠BAD=90°,AB=2,CD=1,△ADE是边长为2的正三角形.现将△ADE沿AD折起,得到四棱锥E﹣ABCD(如图2),且DE⊥AB.
(Ⅰ)求证:平面ADE⊥平面ABCD;
(Ⅱ)求平面BCE和平面ADE所成锐二面角的大小;
(Ⅲ)在棱AE上是否存在点F,使得DF∥平面BCE?若存在,求 ![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.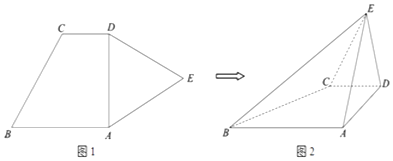
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD﹣A1B1C1D1中,E、F分别为棱DD1和BC中点G为棱A1B1上任意一点,则直线AE与直线FG所成的角为( ) 
A.30°
B.45°
C.60°
D.90°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com