
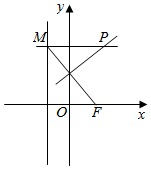
 在平面直角坐标系xOy中,点F(1,0),直线x=-1与动直线y=n的交点为M,线段MF的中垂线与动直线y=n的交点为P.
在平面直角坐标系xOy中,点F(1,0),直线x=-1与动直线y=n的交点为M,线段MF的中垂线与动直线y=n的交点为P.分析 (Ⅰ)连接PF,运用中垂线的性质可得|MP|=|PF|,再由抛物线的定义可得点P的轨迹方程;
(Ⅱ)求得M(-1,n),过点M的切线斜率存在,设为k,则切线方程为:y-n=k(x+1),联立抛物线的方程,消去y,运用相切的条件:判别式为0,再由韦达定理,结合两直线垂直的条件:斜率之积为-1,即可得证.
解答 解:(Ⅰ)据题意,MP⊥直线x=-1,
∴|MP|为点P到直线x=-1的距离,
连接PF,∵P为线段MF的中垂线与直线y=n的交点,
∴|MP|=|PF|,
∴P点的轨迹是抛物线,焦点为F(1,0),准线为直线x=-1,
∴曲线Г的方程为y2=4x;
(Ⅱ)证明:据题意,M(-1,n),过点M的切线斜率存在,设为k,
则切线方程为:y-n=k(x+1),
联立抛物线方程$\left\{\begin{array}{l}{y=kx+k+n}\\{{y}^{2}=4x}\end{array}\right.$
可得ky2-4y+4k+4n=0,
由直线和抛物线相切,
可得△=16-4k(4k+4n)=0,
即k2+kn-1=0,(*)
∵△=n2+4>0,∴方程(*)存在两个不等实根,设为k1,k2,
∵k1=kAM,k2=kBM,
由方程(*)可知,kAM•kBM=k1•k2=-1,
∴切线AM⊥BM,∴∠AMB=90°,结论得证.
点评 本题考查轨迹方程的求法,注意运用抛物线的定义,考查直线和抛物线方程联立,运用直线和抛物线相切的条件:判别式为0,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | p为真 | B. | q为真 | C. | p∧q为假 | D. | p∨q为真 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a>b,c>d,则a-c>b-d | B. | 若a>b,c>d,则ac>bd | ||
| C. | 若$\frac{1}{a}$<$\frac{1}{b}$<0,则ab<b2 | D. | 若$\frac{b}{a}$>$\frac{b-1}{a-1}$,则a>b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com